SOCR EduMaterials Activities ConfidenceIntervals
From Socr
SOCR Educational Materials - Activities - SOCR Confidence Intervals Activity
URL Go to: http://www.socr.ucla.edu/htmls/SOCR_Experiments.html
- To begin: Choose the Confidence Interval (CI) Experiment. In this experiment you will investigate the empirical properties of the sample-size, confidence level, the size of the constructed confidence interval and the practical utilization of Confidence Intervals in statistical data analysis
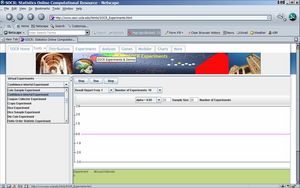
- Exercise 1: Chose the confidence level (α), the sample-size and the number of experiments (see the image below). Click on the <STEP> button - this performs one set of experiments (20 in this case). Each experiment consist of generating a random sample of the given size (5, in this case) from the standard Normal Distribution, N(0,1). The samples along with the constructed confidence intervals are then displayed. Notice the experiments that have a green dot below the corresponding confidence intervals. These are the cases where the parameter being estimated by the confidence interval (population mean, in this case) is outside the corresponding confidence interval (above the right-CI-limit, or below the left-CI-limit).
You can use the <SHAPSHOT> button to save as a JPEG image the state of your SOCR experiment on your local computer. The <RUN> allows you to sequantially run large number of sets of experiments (determined by the <Number of Experiments> selection) and monitor the results. Also, the text-area on the bottom of the applet summarizes the results of these experiments.
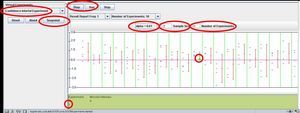
- Question 1: Would you get the same results (what are the results?) if you did this again? If someone else did this? Explain!
- Exercise 2: Now change the sample-size (from 5 to 35) and press <STEP>, or <RUN>. You will notice that the result of the experiment changes significantly (e.g., we have 35 randomly sampled observations plotted in each of the 20 experiments). Also, observe the new summary statistics on the bottom.
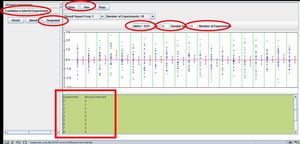
- Question 2: Does the fact that we increased (to 35) the sample-size caused the lack of green-dots (indicators of CIs that do not contain the estimated parameter, μ=0) on this outcome?
How are the CI widths effected by this sample-size increase? Is there a theoretical reason for this observation? Explain! Are we more or less likely to get extreme observations now (sample-size=35) than before (when the sample-size=5)?
- Exercise 3: Finally try changing the alpha-level (α) and the number of experiments? What effects can you predict?
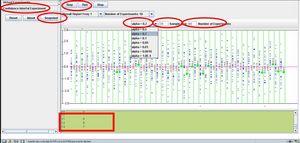
- Question 3: Do you expect an effect on the amount or frequency of the green-dots, when y ou alter the values for α and number of experiments?
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
