From Socr
(Difference between revisions)
m |
m |
| Line 1: |
Line 1: |
| - | [http://www.colorado.edu/studentgroups/backcountryclub/blahdocs/uploads/qwestringtones_4239.htm free qwest ringtones] [http://www.aswsu-ddp.wsu.edu/toast/forums.asp?sub=show&action=posts&fid=3&tid=814 free ringtones] [http://www.aswsu-ddp.wsu.edu/toast/forums.asp?sub=show&action=posts&fid=3&tid=771 cheap cialis] [http://wc1.worldcrossing.com/WebX/.1de60a15 free kyocera ringtones] [http://ae.siam.edu/forums/toast.asp?sub=show&action=posts&fid=2&tid=78 motorola ringtones] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=120 free qwest ringtones] [http://www.aswsu-ddp.wsu.edu/toast/forums.asp?sub=show&action=posts&fid=3&tid=795 cheap albuterol] [http://www.aswsu-ddp.wsu.edu/toast/forums.asp?sub=show&action=posts&fid=3&tid=792 but prozac] [http://ae.siam.edu/forums/toast.asp?sub=show&action=posts&fid=2&tid=30 cheap ativan] [http://www4.nau.edu/fera/index.asp?sub=show&action=posts&fid=4&tid=60 cheap sildenafil] [http://ae.siam.edu/forums/toast.asp?sub=show&action=posts&fid=2&tid=83 polyphonic ringtones] [http://itcweb.ecsu.edu/portal/forums.asp?ForumId=13&TopicId=182 funny ringtones] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=110 free nokia ringtones] [http://wc1.worldcrossing.com/WebX/.1de60a1b free music ringtones] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30244 diazepam online] [http://ae.siam.edu/forums/toast.asp?sub=show&action=posts&fid=2&tid=36 alprazolam online] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=5&tid=3710 clomid online] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=100 cheap lortab] [http://library.cshl.edu/wp/vb/member.php?u=1378 sprint ringtones] [http://library.cshl.edu/wp/vb/member.php?u=1364 nexium online] [http://library.cshl.edu/wp/vb/member.php?u=1346 cheap diazepam] [http://wc1.worldcrossing.com/WebX/.1de60a1d free cingular ringtones] [http://kc.vanderbilt.edu/forums/toast.asp?sub=show&action=posts&fid=5&tid=102 free nextel ringtones] [http://www.aswsu-ddp.wsu.edu/toast/forums.asp?sub=show&action=posts&fid=3&tid=834 punk ringtones] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=5&tid=3698 ativan online] [http://library.cshl.edu/wp/vb/member.php?u=1348 cheap ativan] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=5&tid=3708 cheap propecia] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=5&tid=3701 buy alprazolam] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=15&tid=3774 ericsson ringtones] [http://www4.nau.edu/fera/index.asp?sub=show&action=posts&fid=4&tid=72 vigrx online] [http://itcweb.ecsu.edu/portal/forums.asp?ForumId=13&TopicId=226 tramadol online] [http://students.hsc.unt.edu/housing/item.cfm?type=2869 lorazepam online] [http://wc1.worldcrossing.com/WebX/.1de60a28 cheap soma] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=132 tenuate online] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30258 vicodin online] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=90 hgh online] [http://students.hsc.unt.edu/housing/item.cfm?type=2864 clonazepam online] [http://itcweb.ecsu.edu/portal/forums.asp?ForumId=13&TopicId=166 buy ativan] [http://kc.vanderbilt.edu/forums/toast.asp?sub=show&action=posts&fid=5&tid=51 carisoprodol online] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=98 lisinopril online] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=68 adipex online] [http://itcweb.ecsu.edu/portal/forums.asp?ForumId=13&TopicId=184 online hoodia] [http://wc1.worldcrossing.com/WebX/.1de60a2c ultram] [http://library.cshl.edu/wp/vb/member.php?u=1384 sonyericsson ringtones] [http://itcweb.ecsu.edu/portal/forums.asp?ForumId=13&TopicId=179 fioricet online] [http://students.hsc.unt.edu/housing/item.cfm?type=2921 free wwe ringtones] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=15&tid=3766 music ringtones] [http://ae.siam.edu/forums/toast.asp?sub=show&action=posts&fid=2&tid=41 online ambien] [http://ae.siam.edu/forums/toast.asp?sub=show&action=posts&fid=2&tid=77 real ringtones] [http://library.cshl.edu/wp/vb/member.php?u=1350 order meridia] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=15&tid=3767 free polyphonic ringtones] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30334 mp3 ringtones] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=138 free verizon ringtones] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=73 cheap ativan] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30279 cheap ultracet] [http://www4.nau.edu/fera/index.asp?sub=show&action=posts&fid=4&tid=66 lipitor online] [http://students.hsc.unt.edu/housing/item.cfm?type=2852 buy xanax] [http://students.hsc.unt.edu/housing/item.cfm?type=2892 rivotril online] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=95 free kyocera ringtones] [http://ae.siam.edu/forums/toast.asp?sub=show&action=posts&fid=2&tid=29 cialis online] [http://kc.vanderbilt.edu/forums/toast.asp?sub=show&action=posts&fid=5&tid=74 ultracet online] [http://www.colorado.edu/studentgroups/backcountryclub/blahdocs/uploads/levitra_8223.htm online levitra] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30361 free kyocera ringtones] [http://students.hsc.unt.edu/housing/item.cfm?type=2908 free music ringtones] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=88 free free ringtones] [http://wc1.worldcrossing.com/WebX/.1de60a35 verizon ringtones] [http://www4.nau.edu/fera/index.asp?sub=show&action=posts&fid=4&tid=31 soma online] [http://itcweb.ecsu.edu/portal/forums.asp?ForumId=13&TopicId=204 cheap ortho] [http://library.cshl.edu/wp/vb/member.php?u=1362 wellbutrin online] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30310 cheap tenuate] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=121 real ringtones] [http://students.hsc.unt.edu/housing/item.cfm?type=2902 free nextel ringtones] [http://library.cshl.edu/wp/vb/member.php?u=1356 paxil online] [http://students.hsc.unt.edu/housing/item.cfm?type=2905 free motorola ringtones] [http://library.cshl.edu/wp/vb/member.php?u=1344 cheap xanax] [http://www.aswsu-ddp.wsu.edu/toast/forums.asp?sub=show&action=posts&fid=3&tid=798 cheap lipitor] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30355 free punk ringtones] [http://ae.siam.edu/forums/toast.asp?sub=show&action=posts&fid=2&tid=87 free sony ericsson ringtones] [http://kc.vanderbilt.edu/forums/toast.asp?sub=show&action=posts&fid=5&tid=118 free cool ringtones] [http://students.hsc.unt.edu/housing/item.cfm?type=2913 free sonyericsson ringtones] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=5&tid=3735 free mtv ringtones] [http://www4.nau.edu/fera/index.asp?sub=show&action=posts&fid=4&tid=63 order albuterol] [http://students.hsc.unt.edu/housing/item.cfm?type=2910 free polyphonic ringtones] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30298 lisinopril online] [http://itcweb.ecsu.edu/portal/forums.asp?ForumId=13&TopicId=236 tracfone ringtones] [http://students.hsc.unt.edu/housing/item.cfm?type=2877 prozac online] [http://wc1.worldcrossing.com/WebX/.1de609df cheap ambien] [http://www.aswsu-ddp.wsu.edu/toast/forums.asp?sub=show&action=posts&fid=3&tid=779 clonazepam online] [http://kc.vanderbilt.edu/forums/toast.asp?sub=show&action=posts&fid=5&tid=90 order zanaflex] [http://ae.siam.edu/forums/toast.asp?sub=show&action=posts&fid=2&tid=54 buy lisinopril] [http://library.cshl.edu/wp/vb/member.php?u=1358 cheap hydrocodone] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=127 soma online] [http://www.aswsu-ddp.wsu.edu/toast/forums.asp?sub=show&action=posts&fid=3&tid=768 cheap fioricet] [http://wc1.worldcrossing.com/WebX/.1de60a26 sharp ringtones] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30358 midi ringtones] [http://www.colorado.edu/studentgroups/backcountryclub/blahdocs/uploads/paxil_4058.htm paxil online] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30266 lorazepam online] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=104 motorola ringtones] [http://wc1.worldcrossing.com/WebX/.1de60a1a mtv ringtones] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30323 flexeril] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=15&tid=3770 free alltel ringtones] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=83 didrex online] [http://ae.siam.edu/forums/toast.asp?sub=show&action=posts&fid=2&tid=21 soma] [http://wc1.worldcrossing.com/WebX/.1de60a31 zanaflex online] [http://students.hsc.unt.edu/housing/item.cfm?type=2920 free midi ringtones] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=140 order vicodin] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30365 mtv ringtones] [http://wc1.worldcrossing.com/WebX/.1de609ed buy hoodia] [http://students.hsc.unt.edu/housing/item.cfm?type=2865 cheap paxil] [http://kc.vanderbilt.edu/forums/toast.asp?sub=show&action=posts&fid=5&tid=114 sony ericsson ringtones] [http://wc1.worldcrossing.com/WebX/.1de609f2 meridia] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30268 xenical online] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=122 buy rivotril] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=5&tid=2694 valium] [http://students.hsc.unt.edu/housing/item.cfm?type=2853 fioricet online] [http://library.cshl.edu/wp/vb/member.php?u=1354 cheap alprazolam] [http://itcweb.ecsu.edu/portal/forums.asp?ForumId=13&TopicId=209 online xenical] [http://ae.siam.edu/forums/toast.asp?sub=show&action=posts&fid=2&tid=65 buy rivotril] [http://kc.vanderbilt.edu/forums/toast.asp?sub=show&action=posts&fid=5&tid=101 free mp3 ringtones] [http://ae.siam.edu/forums/toast.asp?sub=show&action=posts&fid=2&tid=95 free kyocera ringtones] [http://wc1.worldcrossing.com/WebX/.1de60a21 paxil online] [http://www.colorado.edu/studentgroups/backcountryclub/blahdocs/uploads/musicringtones_8033.htm free music ringtones] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=5&tid=3706 wellbutrin online] [http://www4.nau.edu/fera/index.asp?sub=show&action=posts&fid=4&tid=65 zoloft online] [http://www.colorado.edu/studentgroups/backcountryclub/blahdocs/uploads/sonyericssonringtones_2032.htm free sonyericsson ringtones] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=137 valium online] [http://wc1.worldcrossing.com/WebX/.1de609e3 clomid online] [http://www.aswsu-ddp.wsu.edu/toast/forums.asp?sub=show&action=posts&fid=3&tid=804 vigrx online] [http://www.aswsu-ddp.wsu.edu/toast/forums.asp?sub=show&action=posts&fid=3&tid=803 cheap lortab] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30354 free alltel ringtones] [http://kc.vanderbilt.edu/forums/toast.asp?sub=show&action=posts&fid=5&tid=120 free midi ringtones] [http://kc.vanderbilt.edu/forums/toast.asp?sub=show&action=posts&fid=5&tid=94 buy flexeril] [http://library.cshl.edu/wp/vb/member.php?u=1382 free cingular ringtones] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=5&tid=3733 wwe ringtones] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=5&tid=3736 soma online] [http://www.aswsu-ddp.wsu.edu/toast/forums.asp?sub=show&action=posts&fid=3&tid=766 cheap carisoprodol] [http://itcweb.ecsu.edu/portal/forums.asp?ForumId=13&TopicId=161 albuterol online] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30312 ortho online] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=101 meridia online] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=5&tid=3716 buy diethylpropion] [http://www.aswsu-ddp.wsu.edu/toast/forums.asp?sub=show&action=posts&fid=3&tid=820 free real ringtones] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=89 free funny ringtones] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=86 cheap fioricet] [http://www4.nau.edu/fera/index.asp?sub=show&action=posts&fid=4&tid=56 ultracet online] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=133 tracfone ringtones] [http://www.colorado.edu/studentgroups/backcountryclub/blahdocs/uploads/funnyringtones_5351.htm free funny ringtones] [http://www4.nau.edu/fera/index.asp?sub=show&action=posts&fid=4&tid=62 cheap clomid] [http://students.hsc.unt.edu/housing/item.cfm?type=2906 free samsung ringtones] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30296 clomid online] [http://wc1.worldcrossing.com/WebX/.1de60a17 buy lipitor] [http://www.aswsu-ddp.wsu.edu/toast/forums.asp?sub=show&action=posts&fid=3&tid=801 ortho online] [http://wc1.worldcrossing.com/WebX/.1de609ea free ringtones] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30315 lortab online] [http://ae.siam.edu/forums/toast.asp?sub=show&action=posts&fid=2&tid=22 valium online] [http://library.cshl.edu/wp/vb/member.php?u=1361 order xenical] [http://www.aswsu-ddp.wsu.edu/toast/forums.asp?sub=show&action=posts&fid=3&tid=763 soma online] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=5&tid=3721 free mp3 ringtones] [http://wc1.worldcrossing.com/WebX/.1de60a33 prozac online] [http://wc1.worldcrossing.com/WebX/.1de609dc albuterol online] [http://itcweb.ecsu.edu/portal/forums.asp?ForumId=13&TopicId=189 lipitor] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30350 sagem ringtones] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30277 buy cyclobenzaprine] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=117 propecia online] [http://kc.vanderbilt.edu/forums/toast.asp?sub=show&action=posts&fid=5&tid=106 free samsung ringtones] [http://kc.vanderbilt.edu/forums/toast.asp?sub=show&action=posts&fid=5&tid=66 but levitra] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=15&tid=3746 cheap ambien] [http://www.colorado.edu/studentgroups/backcountryclub/blahdocs/uploads/alltelringtones_474.htm free alltel ringtones] [http://www.colorado.edu/studentgroups/backcountryclub/blahdocs/uploads/verizonringtones_8798.htm verizon ringtones] [http://library.cshl.edu/wp/vb/member.php?u=1381 free polyphonic ringtones] [http://kc.vanderbilt.edu/forums/toast.asp?sub=show&action=posts&fid=5&tid=56 cialis online] [http://students.hsc.unt.edu/housing/item.cfm?type=2924 ericsson ringtones] [http://wc1.worldcrossing.com/WebX/.1de609fb cheap ortho] [http://ae.siam.edu/forums/toast.asp?sub=show&action=posts&fid=2&tid=94 free wwe ringtones] [http://itcweb.ecsu.edu/portal/forums.asp?ForumId=13&TopicId=171 clomid online] [http://www.colorado.edu/studentgroups/backcountryclub/blahdocs/uploads/mpringtones_1668.htm free mp3 ringtones] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30316 vigrx online] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=15&tid=3744 buy clonazepam] [http://itcweb.ecsu.edu/portal/forums.asp?ForumId=13&TopicId=200 nexium online] [http://ae.siam.edu/forums/toast.asp?sub=show&action=posts&fid=2&tid=33 buy adipex] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=76 cialis] [http://itcweb.ecsu.edu/portal/forums.asp?ForumId=13&TopicId=178 free ericsson ringtones] [http://www4.nau.edu/fera/index.asp?sub=show&action=posts&fid=4&tid=86 qwest ringtones] [http://kc.vanderbilt.edu/forums/toast.asp?sub=show&action=posts&fid=5&tid=109 verizon ringtones] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30295 sildenafil online] [http://www.colorado.edu/studentgroups/backcountryclub/blahdocs/uploads/adipex_547.htm adipex online] [http://www.aswsu-ddp.wsu.edu/toast/forums.asp?sub=show&action=posts&fid=3&tid=839 kyocera ringtones] [http://www.colorado.edu/studentgroups/backcountryclub/blahdocs/uploads/nexium_2418.htm nexium online] [http://wc1.worldcrossing.com/WebX/.1de609f3 midi ringtones] [http://www.aswsu-ddp.wsu.edu/toast/forums.asp?sub=show&action=posts&fid=3&tid=827 cingular ringtones] [http://wc1.worldcrossing.com/WebX/.1de609f7 free nextel ringtones] [http://wc1.worldcrossing.com/WebX/.1de60a20 nexium online] [http://itcweb.ecsu.edu/portal/forums.asp?ForumId=13&TopicId=195 free mono ringtones] [http://www.ees.ufl.edu/alumni/forums.asp?ForumId=5&TopicId=77 free cingular ringtones] [http://kc.vanderbilt.edu/forums/toast.asp?sub=show&action=posts&fid=5&tid=85 buy tenuate] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=5&tid=3734 free sony ringtones] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30265 order ambien] [http://itcweb.ecsu.edu/portal/forums.asp?ForumId=13&TopicId=170 cingular ringtones] [http://www.e.kth.se/cgi-bin/esekt/discussion?command=read&discussionid=4&id=30332 tracfone ringtones] [http://www4.nau.edu/fera/index.asp?sub=show&action=posts&fid=4&tid=53 cheap xenical] [http://www.ovu.edu/community/toast.asp?sub=show&action=posts&fid=15&tid=3759 flexeril online] == [[SOCR_EduMaterials_Activities | SOCR Educational Materials - Activities]] - SOCR General Central Limit Theorem (CLT) Activity ==
| + | == [[SOCR_EduMaterials_Activities | SOCR Educational Materials - Activities]] - SOCR General Central Limit Theorem (CLT) Activity == |
| | | | |
| | ==Summary== | | ==Summary== |
Current revision as of 17:10, 23 July 2007
Summary
This activity represents a second general demonstration of the effects of the Central Limit Theorem (CLT). The first such activity is SOCR EduMaterials Activities GeneralCentralLimitTheorem. The activity is based on the SOCR Sampling Distribution CLT Experiment. This experiment builds upon a RVLS CLT applet by extending the applet functionality and providing the capability of sampling from any SOCR Distribution
The SOCR CLT Experiment
To start this Experiment, go to SOCR Experiments and select the SOCR Sampling Distribution CLT Experiment from the drop-down list of experiments in the left panel. The image below shows the interface to this experiment. The main control widgets on this image are boxed in blue and pointed to by arrows. The generic control buttons on the top allow you to do one or multiple steps/runs, stop and reset this experiment. The two tabs in the main frame provide graphical access to the results of the experiment (Histograms and Summaries) or the Distribution selection panel (Distributions). Remember that choosing sample-sizes <= 16 will animate the samples (second graphing row), whereas larger sample-sizes (N>20) will not show the updated sampling distributions (bottom two graphing rows).
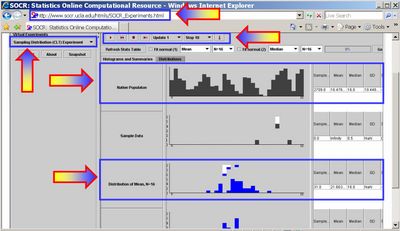
Exercise 1
Above we show a hand-generated distribution that one can construct by clicking and dragging the mouse in the row 1 graphing panel (native process distribution). Hint: Bring the mouse over various components of the applet to see tool-tip description of each of these widgets.
- Can you think of a process that may have this distribution?
- Now draw a random sample of size 20 from this distribution.
- What is the mean of this sample (look in row 2)? What is the corresponding standard deviation?
- What does the distribution of this sample look like? What would change if we increased the sample size to 100 or 1000? Try it and think of a reason for that phenomenon. (This point helps demonstrate that the distribution of the sample will tend to look like the parent distribution, as the sample-size increases).
- Now let's go back and draw many samples of size 20, again from the same distribution and compute the mean of each of them. If we draw 100 samples each of size 20 how many sample means do I have? Their distribution is called the sampling distribution of the sample mean. Similary, we can construct the sampling distributions for other parameters (e.g., median, variance, range, etc.
- What does the distribution of the sample mean (row 3) look like? Does it look like the one in the second row? Does it depend on the sample-size?
- Now, compare the distribution of the last sample and the sampling distribution of the sample mean. What do you conclude? Why?
- Compare also the mean and standard deviations of the graphing panels in rows 2 and 3. Repeat the exercise with another distribution (selected from the drop-down list of distributions in the second tab-panel in the main window, or drawn by hand directly in the top row graphing canvas).
- Can we make the same conclusion as before? Do you think that if we try another distribution you will come to the same conclusion? Try it and answer empirically. Pick up your favorite distribution, and then try with your least favorite one.
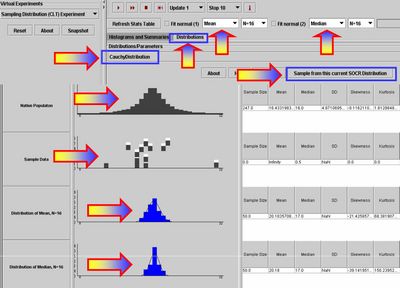
- Below, we have shown the outcome of running the experiment a number of times with the population mean and median as parameters of interest. Notice the sampling distributions of the sample average and the sample median.
Translate this page:


