SOCR EduMaterials Activities JointDistributions
From Socr
This is an activity to explore the joint distributions of X and Y through two simple examples.
- Description: You can access the applets for the following experiments at SOCR Experiments
- Exercise 1: Die coin experiment:
A die is rolled and the number observed X is recorded. Then a coin is tossed number of times equal to the value of X. For example if X = 2 then the coin is tossed twice, etc. Let Y be the number of heads observed. Note: Assume that the die and the coin are fair.
- 1. Construct the joint probability distribution of X and Y.
- 2. Find the conditional expected value of Y given X = 5.
- 3. Find the conditional variance of Y given X = 5.
- 4. Find the expected value of Y.
- 5. Find the standard deviation of Y.
- 6. Graph the probability distribution of Y.
- 7. Use SOCR to graph and print the empirical distribution of Y when the experiment is performed
- a. n = 1000 times.
- b. n = 10000 times.
- 8. Compare the theoretical mean and standard deviation of Y (parts (4) and (5)) with the empirical mean and standard deviation found in part (8).
Below you can see a snapshot of the theoretical distribution of Y.
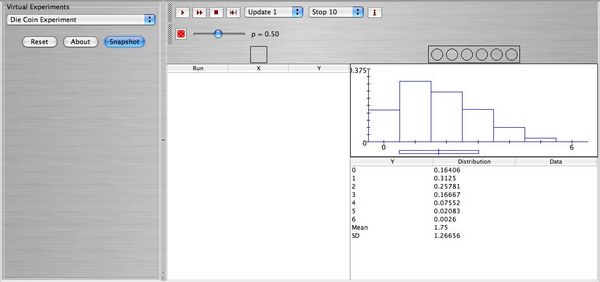
- Exercise 2: Coin Die experiment:
A coin is tossed and if heads is observed then a red die is rolled. If tails is observed then a green die is rolled. You can choose the distribution of each die as well as the probability of heads. Choose for the red die the 3-4 flat distribution and for the green die the skewed right distribution. Finally using the scroll button choose $p=0.2$ as the probability of heads. Let X be the score of the coin (1 for heads, 0 for tails), and let Y be the score of the die (1,2,3,4,5,6).
- 1. Construct the joint probability distribution of X,Y.
- 2. Find the marginal probability distribution of Y and verify that it is the same with the one given in the applet.
- 3. Compute E(Y).
- 4. Compute E(Y) using expectation by conditioning E[E(Y | X)].
- 5. Run the experiment 1000 times take a snapshot and comment on the results.
Below you can see a snapshot of the theoretical distribution of Y.
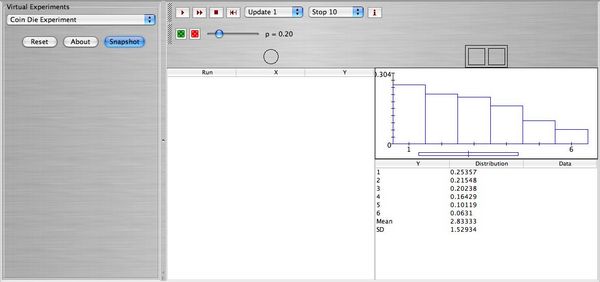
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
