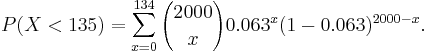SOCR EduMaterials Activities Normal Probability examples
From Socr
Contents |
SOCR Distribution Activities - Normal Distribution Examples
You should first review the complete details about the Standard Normal and the General Normal distributions. Also, refer to the interactive web-based SOCR Distribution applets.
Example 1
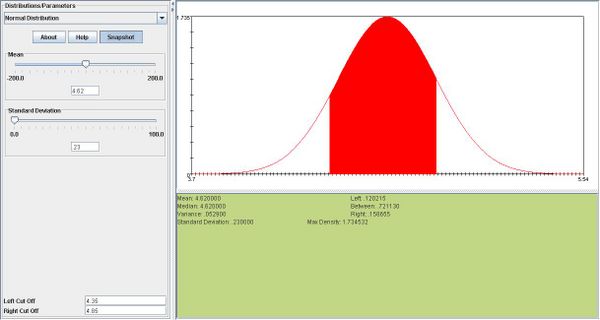
- The lengths of the sardines received by a certain cannery is normally distributed with mean 4.62 inches and a standard deviation 0.23 inch. What percentage of all these sardines is between 4.35 and 4.85 inches long?
Solution
- We are given
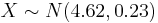 . We want to compute
. We want to compute
- We are given
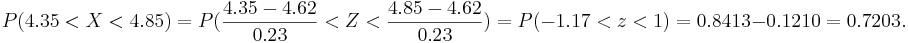
Example 2
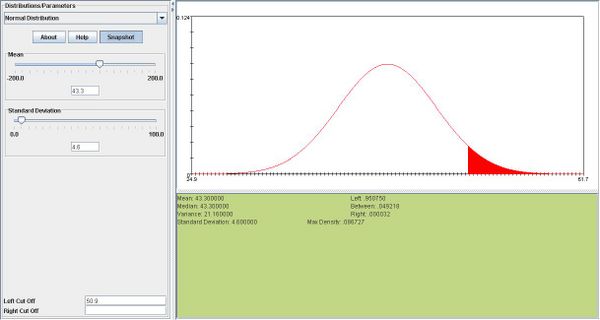
- A baker knows that the daily demand for apple pies is a random variable which follows the normal distribution with mean 43.3 pies and standard deviation 4.6 pies. Find the demand which has probability 5% of being exceeded.
Solution
- We are given
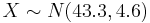 . We want to find the demand d such that P(X > d) = 0.05. From the standard normal table this corresponds to
. We want to find the demand d such that P(X > d) = 0.05. From the standard normal table this corresponds to
- We are given
z = 1.645. Therefore 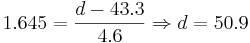 pies.
pies.
Example 3
- Suppose that the height of UCLA female students has normal distribution with mean 62 inches and standard deviation 8 inches.
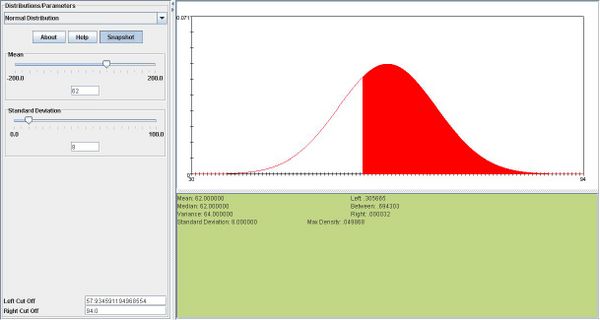
- a. Find the height below which is the shortest 30% of the female students.
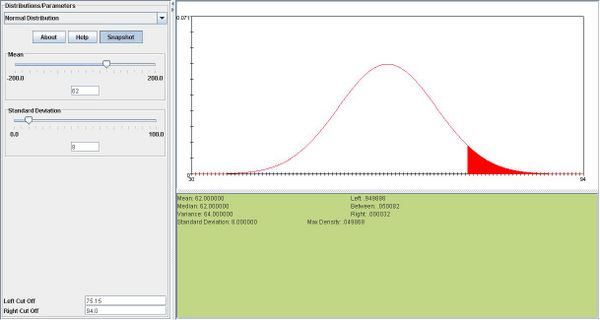
- b. Find the height above which is the tallest 5% of the female students.
Solution
- a.We are given
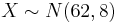 . We want to find the height h such that P(X < h) = 0.30. From the
. We want to find the height h such that P(X < h) = 0.30. From the
standard normal table this corresponds to z = − 0.525. Therefore 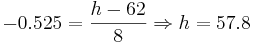 inches.
inches.
- b. We want to find the height h such that P(X > h) = 0.05. From the standard normal table this corresponds to z = 1.645.
Therefore 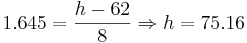 inches.
inches.
Example 4
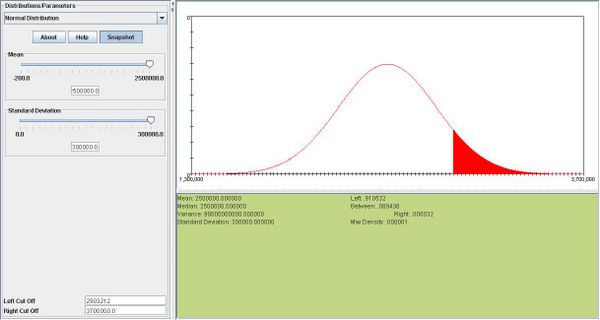
- A firm's marketing manager believes that total sales for next year will follow the normal distribution, with mean of $2.5 million and a standard deviation of $300, 000.
- a. What is the probability that the firm's sales will fall within $150000 of the mean?
- b.Determine the sales level that has only a 9% chance of being exceeded next year.
Solution
- a. We are given
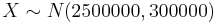 .
.
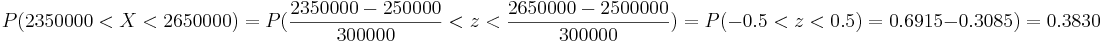 .
.
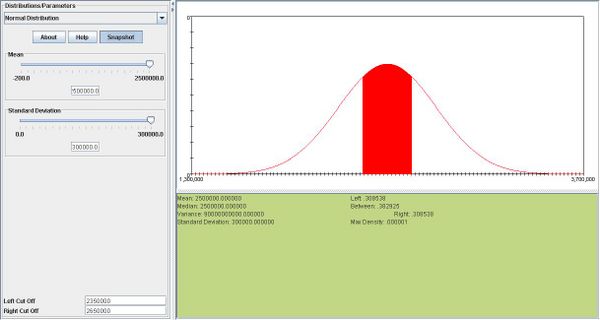
- b. We want to find the sales level s such that P(X > s) = 0.09.
This corresponds to z = 1.345.
- Therefore
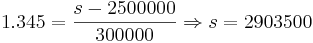 .
.
- Therefore
Example 5
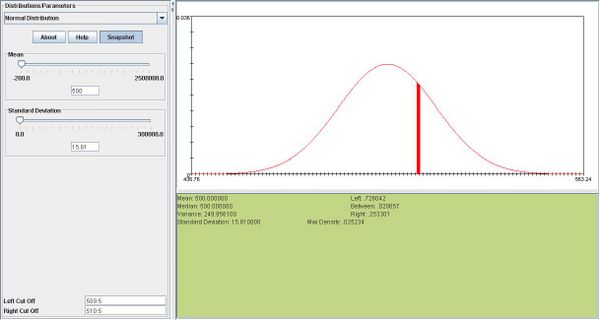
- To avoid accusations of sexism in a college class equally populated by male and female students, the professor flips a fair coin to decide whether to call upon a male or female student to answer a question directed to the class. The professor will call upon a female student if a tails occurs. Suppose the professor does this 1000 times during the semester.
- a. What is the probability that he calls upon a female student at least 530 times?
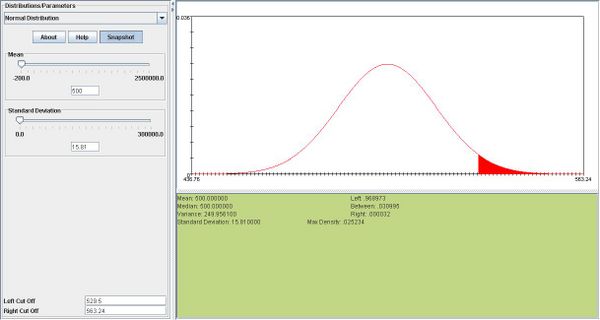
- b. What is the probability that he calls upon a female student at most 480 times?
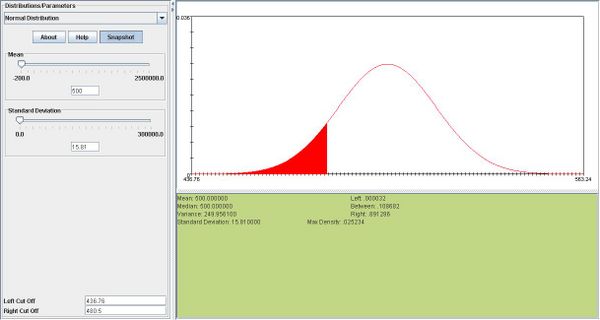
- c. What is the probability that he calls upon a female student exactly 510 times?
Solution
- This is a binomial problem but we are going to use the normal distribution as an approximation. We need μ and σ.
- These are:
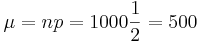 .
.
- And
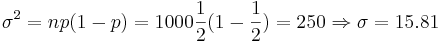 .
.
- a.
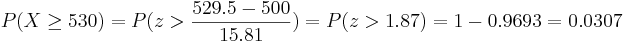 .
.
- b.
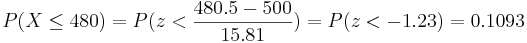 .
.
- c.
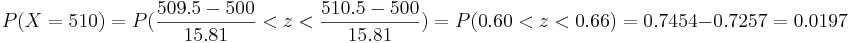 .
.
Example 6
- MENSA is an organization whose members possess IQs in the top 2% of the population.
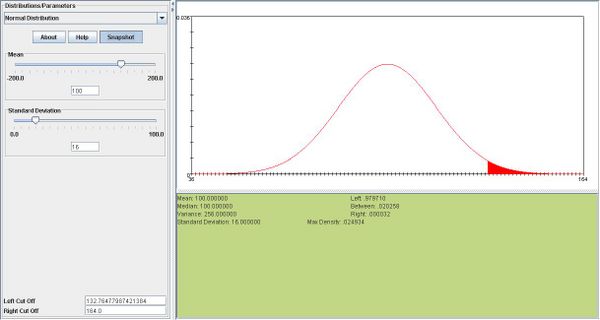
- a. If IQs are normally distributed, with mean 100 and a standard deviation of 16, what is the minimum IQ required for admission to MENSA?
- b. If three individuals are chosen at random from the general population what is the probability that all three satisfy the minimum requirement for MENSA?
Solution
- a. We are given
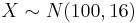 . We want to find the IQ q such that P(X > q) = 0.02. This corresponds to z = 2.055. Therefore
. We want to find the IQ q such that P(X > q) = 0.02. This corresponds to z = 2.055. Therefore 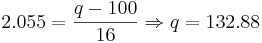 .
.
- b. This is binomial with
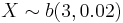 . We want
. We want
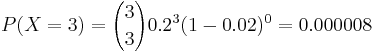 .
.
Example 7
- A manufacturing process produces semiconductor chips with a known failure rate 6.3%. Assume that chip failures are independent of one another. You will be producing 2000 chips tomorrow.
- a. Find the expected number of defective chips produced.
- b. Find the standard deviation of the number of defective chips.
- c. Find the probability (approximate) that you will produce less than 135 defects.
Solution
- This is binomial with
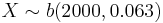 .
.
- This is binomial with
- a. E(X) = np = 2000(0.063) = 126.
- b. σ2 = np(1 − p) = 2000(0.063)(1 − 0.063) = 118.06
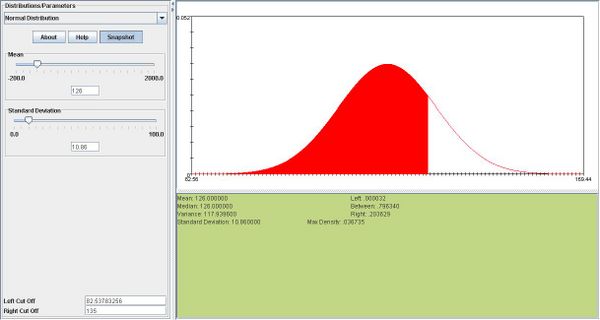
- c.
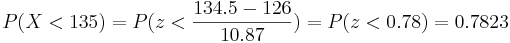 . The exact probability is:
. The exact probability is:
Example 8
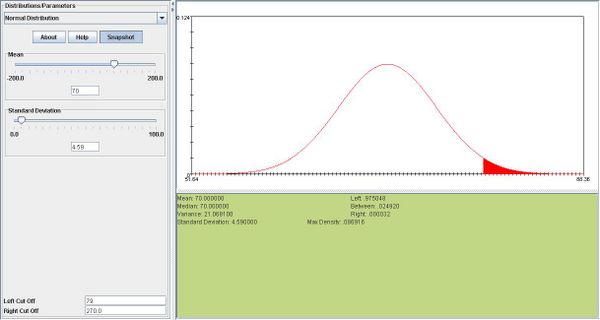
- Suppose that the height (X) in inches, of a 25-year-old man is a normal random variable with mean it = 70 inches. If P(X > 79) = 0.025 what is the standard deviation of this random normal variable?
Solution
- We are given
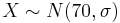 . From P(X > 79) = 0.025 we find the
. From P(X > 79) = 0.025 we find the
- We are given
corresponding z-value: z = 1.96. Therefore
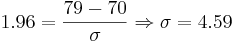 inches.
inches.
Example 9
- Suppose that the weight (X) in pounds, of a 40-year-old man is a normal random variable with standard deviation 20 pounds. If 5% of this population is heavier than 214 pounds what is the mean it of this distribution?
Solution
- We are given
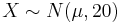 . From P(X > 214) = 0.05 we find the
. From P(X > 214) = 0.05 we find the
- We are given
corresponding z-value: z = 1.645. Therefore
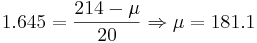 pounds.
pounds.
Example 10
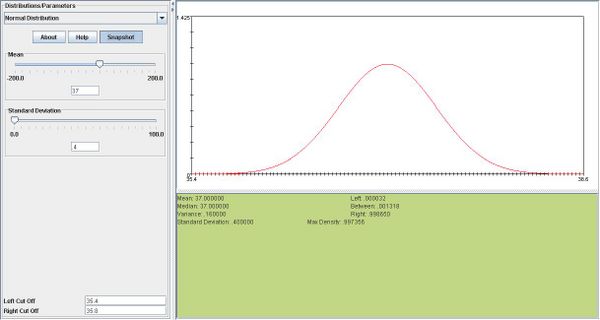
- At Heinz ketchup factory the amounts which go into bottles of ketchup are supposed to be normally distributed with mean 36 oz. and standard deviation 0.1 oz. Once every 30 minutes a bottle is selected from the production line, and its contents are noted precisely. If the amount of the bottle goes below 35.8 oz. or above 36.2 oz., then the bottle will be declared out of control.
- a.If the process is in control, meaning it μ = 36oz. and </math>\sigma= 0.1 oz.</math>, find the probability that a bottle will be declared out of control.
- b. In the situation of (a), find the probability that the number of bottles found out of control in an eight-hour day (16 inspections) will be zero.
- c. In the situation of (a), find the probability that the number of bottles found out of control in an eight-hour day (16 inspections) will be exactly one.
- d. If the process shifts so that it = 37 oz and u = 0.4 oz, find the probability that a bottle will be declared out of control.
Solution
- The process is out of control if P(X < 35.8) or P(X > 36.2).
- a. We are given
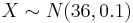 . We compute the probability:
. We compute the probability:
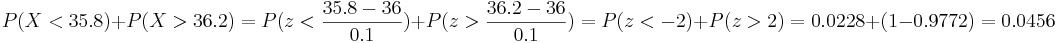 .
.
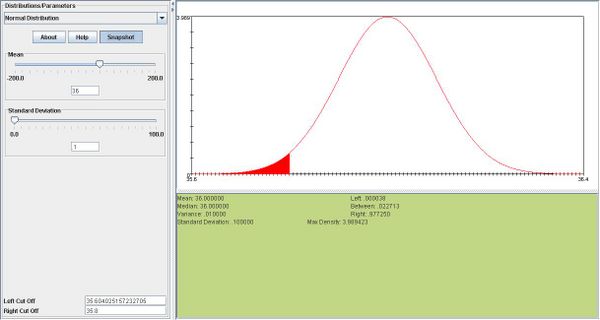
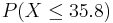
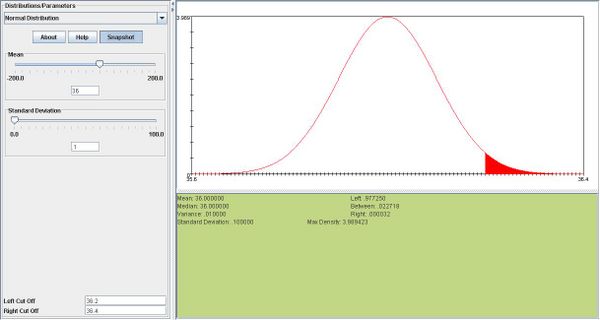
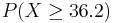 . We add the two probabilities.
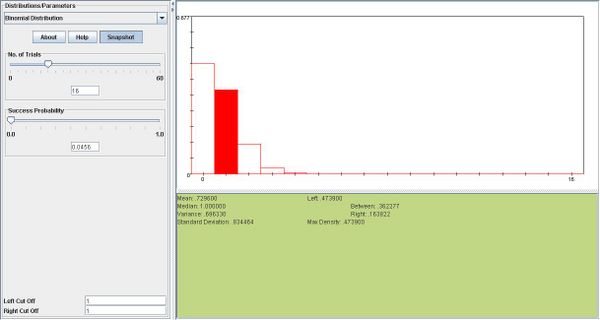
. We add the two probabilities.- b. This is binomial with n = 16,p = 0.0456.
 .
.
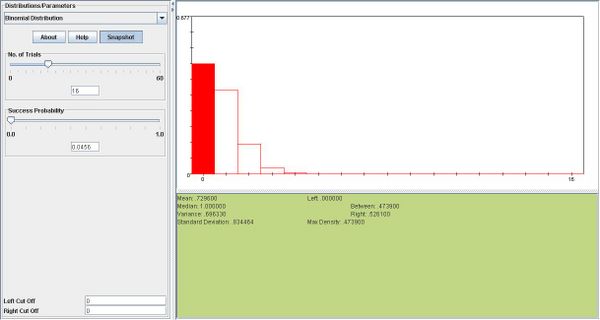
- c. This is binomial with n = 16,p = 0.0456.
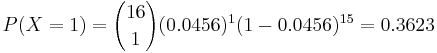 .
.
- d. Now
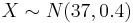 . We compute the probability:
. We compute the probability:
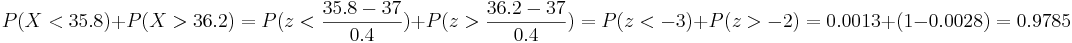 .
.
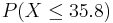 .
.
 . We add the two probabilities.
. We add the two probabilities.Example 11
- Suppose that a binary message -either 0 or 1- must be transmitted by wire from location A to location B. However, the data sent over the wire are subject to a channel noise disturbance, so to reduce the possibility of error, the value 2 is sent over the wire when the message is 1 and the value -2 is sent when the message is O. If x, x = +2, is the value sent from location A, then R, the value received at location B, is given by R = x + N, where N is the channel noise disturbance. When the message is received at location B the receiver decodes it according to the following rule:
- If R > 0.5, then 1 is concluded If R < 0.5, then 0 is concluded
- If the channel noise follows the standard normal distribution compute the probability that the message will be wrong when decoded.
Solution
- The channel noise N follows the standard normal distribution, N(0,1).
- If the message was 1: It will be wrong when decoded if R < 0.5.
Or 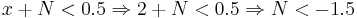 . This
probability is equal to P(z < − 1.5) = 0.0668.
. This
probability is equal to P(z < − 1.5) = 0.0668.
- If the message was 0: It will be wrong when decoded if
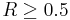 .
.
- If the message was 0: It will be wrong when decoded if
Or 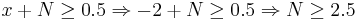 . This
probability is equal to
. This
probability is equal to 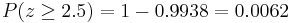 .
.
See also
Translate this page: