SOCR EduMaterials AnalysisActivities HierarchicalClustering
From Socr
Contents |
SOCR Analysis Hierarchical Clustering Analysis Activity
Overview
This SOCR Activity demonstrates the utilization of the SOCR Analyses package for statistical computing. In particular, it shows how to use Hierarchical Clustering and how to interpret the output results.
Background
Hierarchical Clustering is a technique of clustering analysis which aims to build a hierarchy (top-down ordering) of clusters. Hierarchical clustering is classified as a connectivity-based clustering algorithm, as it builds models based on distance connectivity (i.e., distances between different clusters). There are various ways to compute the distances – for example, in the single linkage method, the distance between two clusters is computed as the distance between the two closest elements in the two clusters, whereas in the complete linkage method, it is computed as the distance between the two farthest elements in the two clusters. In essence, the paradigm of hierarchical clustering boils down to the following steps:
- Designate every object/item to a new cluster - if you have X items, then there should be X clusters, with each of them containing just one object.
- Calculate the distances between all the current clusters: If each cluster only contains one object, then the distance between each pair is the same as the distance between the objects they contain. If each cluster contain more than one item, then the distance between each pair can be determined using one of the connectivity based methods: Single linkage, complete linage, unweighted average, weighted average, unweighted centroid, weighted centroid, joint between-within, etc.
- Based on the distances calculated from step 1, find the closest pair of clusters and merge them into a single cluster, so that there is one less cluster now.
- Repeat steps 2 and 3, until all objects are merged into a single cluster of size X.
The results of the above algorithm is usually presented in a dendrogram, which is essentially a tree structure displaying the top-down ordering of clusters under the selected method of distance calculation.
Activity Goals
The goals of this activity are to expose learners to:
- Inputting data in the correct formats;
- Reading results of Hierarchical Clustering;
- Making interpretation of the resulting dendrogram.
Hierarchical Clustering Applet: Data Input
Go to SOCR Analyses and select Hierarchical Clustering from the drop-down list of SOCR analyses, in the left panel. There are two ways to enter data in the SOCR Hierarchical Clustering applet:
- Click on the Example button on the top of the right panel.
- Load a text file containing the correctly formatted data by clicking on “Load” button inside the menu bar of DENDROGRAM panel. See below for currently supported data formats.
- Paste your own data from a spreadsheet into SOCR Hierarchical Clustering data table.
The following is a list of our supported data formats, applying to both ways of inputting (i.e., file “Load” button and copy-paste from spreadsheet).
- Matrix-like file format: Each line in the text file contains a data matrix row. The characteristics of these files are:
- The matrix must be symmetric, and the diagonal elements must be zeros.
- Within each row, the elements are separated by: spaces (‘ ’), tab character, semicolon (‘;’), comma (‘,’) or vertical bar (‘|’).
- It is possible to include the names in an additional first row or column, but not in both.
- If present, the labels of the nodes can not contain any of the previous separators. Some different representations for the previous matrix could be:
| Node_a | Node_b | Node_c | Node_d |
|---|---|---|---|
| 0.0 | 2.0 | 4.0 | 7.0 |
| 2.0 | 0.0 | 2.0 | 5.0 |
| 4.0 | 2.0 | 0.0 | 3.0 |
| 7.0 | 5.0 | 3.0 | 0.0 |
Or it's transpose
| Node_a | 0.0 | 2.0 | 4.0 | 7.0 |
| Node_b | 2.0 | 0.0 | 2.0 | 5.0 |
| Node_c | 4.0 | 2.0 | 0.0 | 3.0 |
| Node_d | 7.0 | 5.0 | 3.0 | 0.0 |
- List-like file format: Each line in the text file contains three elements, which represent the labels of two nodes and the distance (or weight) between them. The characteristics of these files are:
- The separators between the three elements may be: spaces (‘ ’), tab character, semicolon (‘;’), comma (‘,’) or vertical bar (‘|’).
- The labels of the nodes can not contain any of the previous separators.
- Distances from an element to itself (e.g. “a a 0.0”) must not be included.
- The Hierarchical Clustering applet accepts either the presence or absence of the symmetric data elements, i.e., if the distance between nodes a and b is 2.0, it is possible to include in the list the line “a b 2.0”, or both “a b 2.0” and “b a 2.0”. If both are present, the program checks if they are equal.
Input Data examples
The following simple examples demonstrate the three list‐like files discussed above:
- Simple list:
| a | b | 2 |
| a | c | 4 |
| a | d | 7 |
| b | c | 2 |
| b | d | 5 |
| c | d | 3 |
- Complete list:
| a | b | 2 |
| a | c | 4 |
| a | d | 7 |
| b | a | 2 |
| b | c | 2 |
| b | d | 5 |
| c | a | 4 |
| c | b | 2 |
| c | d | 3 |
| d | a | 7 |
| d | b | 5 |
| d | c | 3 |
- Matrix‐like with node labels in the first column, data separated by spaces:
| 0.0 | 2.0 | 4.0 | 7.0 | |||
| 2.0 | 0.0 | 2.0 | 5.0 | |||
| 4.0 | 2.0 | 0.0 | 3.0 | |||
| 7.0 | 5.0 | 3.0 | 0.0 |
Hierarchical Clustering Example: Primate Evolution
We will demonstrate Hierarchical Clustering using a SOCR built-in example. DNA data representing the molecular phylogeny and evolution of primate mitochondrial DNA is obtained from Hayasaka, Gojobori, and Horai (1988). In this homoplasy example, the primate distance matrix was computed by Makarenkov and Legendre, (2004) and is shown below:
- As you start the SOCR Analyses Applet, click on Hierarchical Clustering from the combo box in the left panel. Here's what the screen should look like.
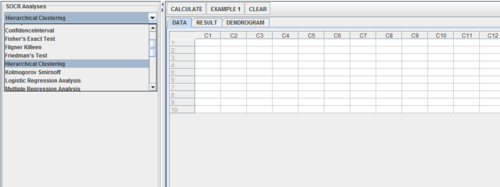
- The left part of the panel looks like this (make sure that the Hierarchical Clustering is showing in the drop-down list of analyses, otherwise you won't be able to find the correct dataset and will not be able to reproduce the results!)
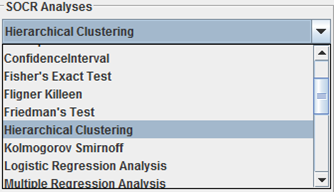
- In the SOCR Hierarchical Clustering analysis, there is one SOCR built-in example. Click on the Example 1 button.
The dendrogram to the right of the menu bar summarizes the results of Hierarchical Clustering analysis (using unweighted average method) nicely. To change the method used to calculate the distances between clusters, click on the drop-down menu to the right of “Clustering Algorithm” inside the menu bar, and you will see a list of supported methods: Single linkage, complete linage, unweighted average, weighted average, unweighted centroid, weighted centroid and joint between-within. After selecting, click on the “Update” button on the top left, and the dendrogram will then be updated according to the method selected. The user can simultaneous load a text file of correctly formatted data without affecting the current open dendrogram.
As you notice, the dendrogram is a preferable way of displaying the algorithm of hierarchical clustering, as it gives the user a birds-eye view of the merging process without losing significant information.
| Species | Homo_sapiens | Pan | Gorilla | Pongo | Hylobates | Macaca_fuscata | Macaca_mulatta | Macaca_fascicular. | Macaca_sylvanus | Saimiri_sciureus | Tarsius_syrichta | Lemur_catta |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Homo_sapiens | 0 | 0.089 | 0.104 | 0.161 | 0.182 | 0.232 | 0.233 | 0.249 | 0.256 | 0.273 | 0.322 | 0.308 |
| Pan | 0.089 | 0 | 0.106 | 0.171 | 0.189 | 0.243 | 0.251 | 0.268 | 0.249 | 0.284 | 0.321 | 0.309 |
| Gorilla | 0.104 | 0.106 | 0 | 0.166 | 0.189 | 0.237 | 0.235 | 0.262 | 0.244 | 0.271 | 0.314 | 0.293 |
| Pongo | 0.161 | 0.171 | 0.166 | 0 | 0.188 | 0.244 | 0.247 | 0.262 | 0.241 | 0.284 | 0.303 | 0.293 |
| Hylobates | 0.182 | 0.189 | 0.189 | 0.188 | 0 | 0.247 | 0.239 | 0.257 | 0.242 | 0.269 | 0.309 | 0.296 |
| Macaca_fuscata | 0.232 | 0.243 | 0.237 | 0.244 | 0.247 | 0 | 0.036 | 0.084 | 0.124 | 0.289 | 0.314 | 0.282 |
| Macaca_mulatta | 0.233 | 0.251 | 0.235 | 0.247 | 0.239 | 0.036 | 0 | 0.093 | 0.12 | 0.293 | 0.316 | 0.289 |
| Macaca_fascicular. | 0.249 | 0.268 | 0.262 | 0.262 | 0.257 | 0.084 | 0.093 | 0 | 0.123 | 0.287 | 0.311 | 0.298 |
| Macaca_sylvanus | 0.256 | 0.249 | 0.244 | 0.241 | 0.242 | 0.124 | 0.12 | 0.123 | 0 | 0.287 | 0.319 | 0.287 |
| Saimiri_sciureus | 0.273 | 0.284 | 0.271 | 0.284 | 0.269 | 0.289 | 0.293 | 0.287 | 0.287 | 0 | 0.32 | 0.285 |
| Tarsius_syrichta | 0.322 | 0.321 | 0.314 | 0.303 | 0.309 | 0.314 | 0.316 | 0.311 | 0.319 | 0.32 | 0 | 0.252 |
| Lemur_catta | 0.308 | 0.309 | 0.293 | 0.293 | 0.296 | 0.282 | 0.289 | 0.298 | 0.287 | 0.285 | 0.252 | 0 |
Below is the same data where all distance matrix values are converted to integers (multiplying the original values by 1,000).
| Species | Homo_sapiens | Pan | Gorilla | Pongo | Hylobates | Macaca_fuscata | Macaca_mulatta | Macaca_fascicular. | Macaca_sylvanus | Saimiri_sciureus | Tarsius_syrichta | Lemur_catta |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Homo_sapiens | 0 | 89 | 104 | 161 | 182 | 232 | 233 | 249 | 256 | 273 | 322 | 308 |
| Pan | 89 | 0 | 106 | 171 | 189 | 243 | 251 | 268 | 249 | 284 | 321 | 309 |
| Gorilla | 104 | 106 | 0 | 166 | 189 | 237 | 235 | 262 | 244 | 271 | 314 | 293 |
| Pongo | 161 | 171 | 166 | 0 | 188 | 244 | 247 | 262 | 241 | 284 | 303 | 293 |
| Hylobates | 182 | 189 | 189 | 188 | 0 | 247 | 239 | 257 | 242 | 269 | 309 | 296 |
| Macaca_fuscata | 232 | 243 | 237 | 244 | 247 | 0 | 36 | 84 | 124 | 289 | 314 | 282 |
| Macaca_mulatta | 233 | 251 | 235 | 247 | 239 | 36 | 0 | 93 | 120 | 293 | 316 | 289 |
| Macaca_fascicular. | 249 | 268 | 262 | 262 | 257 | 84 | 93 | 0 | 123 | 287 | 311 | 298 |
| Macaca_sylvanus | 256 | 249 | 244 | 241 | 242 | 124 | 120 | 123 | 0 | 287 | 319 | 287 |
| Saimiri_sciureus | 273 | 284 | 271 | 284 | 269 | 289 | 293 | 287 | 287 | 0 | 320 | 285 |
| Tarsius_syrichta | 322 | 321 | 314 | 303 | 309 | 314 | 316 | 311 | 319 | 320 | 0 | 252 |
| Lemur_catta | 308 | 309 | 293 | 293 | 296 | 282 | 289 | 298 | 287 | 285 | 252 | 0 |
- You can also load these data in the SOCR 3D Viewer (requires Java 3D) (specify 12x12) to see the distance matrix as an image gradient in 3D.
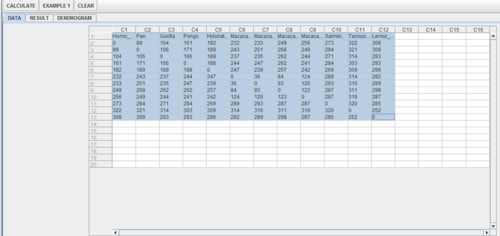
- Load the data into the SOCR Hierarchic Clustering Applet, as shown below:
- Run the clustering analysis to get a result like the hierarchical tree shown below:
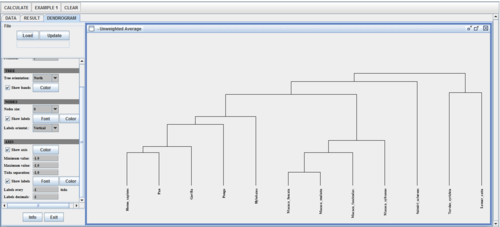
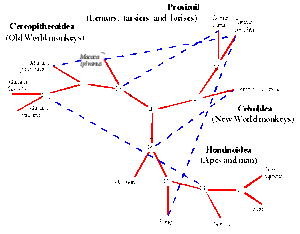
- Note that this classification agrees with the phylogenetic tree hierarchy previously reported:
Note
If you happen to click on the Clear button in the middle of the procedure, all the data will be cleared out. Simply start over from step 1 and click on an EXAMPLE button for the data you want.
See also
References
- Hayasaka, K., Gojobori, T., Horai, S. (1988) Molecular phylogeny and evolution of primate mitochondrial DNA. Molecular Biology and Evolution 5, 626-644.
- Makarenkov, V, Legendre, P. Desdevises, Y. (2004) Modelling phylogenetic relationships using reticulated networks Zoologica Scripta, 33(1):89–96.
Translate this page:
