SOCR EduMaterials FunctorActivities MGF Moments
From Socr
(Difference between revisions)
(New page: == This is an activity to explore useful properties of MGF's.== * '''Description''': You can access the applets for the above distributions at http://www.socr.ucla.edu/htmls/SOCR_Distri...) |
|||
| (2 intermediate revisions not shown) | |||
| Line 2: | Line 2: | ||
* '''Description''': You can access the applets for the above distributions at http://www.socr.ucla.edu/htmls/SOCR_DistributionFunctors.html . | * '''Description''': You can access the applets for the above distributions at http://www.socr.ucla.edu/htmls/SOCR_DistributionFunctors.html . | ||
| + | |||
| + | * '''Exercise 1:''' As you have learned in class, there are quite a few interesting properties that Moment Generating Functions hold. For example you learned that <math> E(X^n)=M_{x}^{(n)}(0)={d^n M_x(t)\over{dt^n}}\mid_{t=0} </math> If the MGF is defined in the neighborhood of 0. So to get the Expected Value for a particular distribution, you would take the first derivative of the MGF and set t=0. Use SOCR to graph and print the following distributions and answer the questions below. ''You must do these exercises using MGF's, you can find the slope using the mouse pointer.'' | ||
| + | **a. Find the Expected Value of <math> X \sim Binomial(10,.5) </math> | ||
| + | **b. Find the Expected Value of <math> X \sim Normal(0,1) </math> | ||
| + | **c. Find the Expected Value of <math> X \sim ChiSquare(13) </math> | ||
| + | |||
| + | * '''Exercise 2:''' Can you use MGF's to find the Expected Value for the Continuous Uniform Distribution? Why or why not? | ||
| + | |||
| + | * '''Exercise 3:''' In Exercise 1, we calculated the <math>1^{st}</math> Moment. If we take the second derivative of the MGF with respect to t, where <math> t=0 </math>. We get <math> E(X^2) </math>. We can use this to find the Variance of a particular Distribution. Repeat Parts (a,b,c) for Exercise 1, but this time calculate the variance. | ||
| + | |||
| + | * '''Exercise 4:''' What do we get when we take the <math>3^{rd}</math> and <math<4^{th}</math> derivatives of a MGF and set <math> t=0 </math>? | ||
| + | |||
| + | ==See also== | ||
| + | * [[SOCR_EduMaterials_FunctorActivities_MGF | Other SOCR Distribution Functor Activities]] | ||
| + | |||
| + | <hr> | ||
| + | * SOCR Home page: http://www.socr.ucla.edu | ||
| + | |||
| + | {{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php?title=SOCR_EduMaterials_FunctorActivities_MGF_Moments}} | ||
Current revision as of 06:23, 9 January 2008
This is an activity to explore useful properties of MGF's.
- Description: You can access the applets for the above distributions at http://www.socr.ucla.edu/htmls/SOCR_DistributionFunctors.html .
- Exercise 1: As you have learned in class, there are quite a few interesting properties that Moment Generating Functions hold. For example you learned that
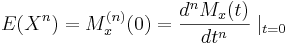If the MGF is defined in the neighborhood of 0. So to get the Expected Value for a particular distribution, you would take the first derivative of the MGF and set t=0. Use SOCR to graph and print the following distributions and answer the questions below. You must do these exercises using MGF's, you can find the slope using the mouse pointer.
- a. Find the Expected Value of
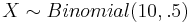
- b. Find the Expected Value of
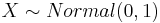
- c. Find the Expected Value of
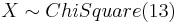
- a. Find the Expected Value of
- Exercise 2: Can you use MGF's to find the Expected Value for the Continuous Uniform Distribution? Why or why not?
- Exercise 3: In Exercise 1, we calculated the 1st Moment. If we take the second derivative of the MGF with respect to t, where t = 0. We get E(X2). We can use this to find the Variance of a particular Distribution. Repeat Parts (a,b,c) for Exercise 1, but this time calculate the variance.
- Exercise 4: What do we get when we take the 3rd and <math<4^{th}</math> derivatives of a MGF and set t = 0?
See also
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
