SOCR Events May2008 C5 S1
From Socr
(Difference between revisions)
(→Estimate the equation of a line of best fit to make and test conjectures) |
|||
| Line 15: | Line 15: | ||
===[[SOCR_EduMaterials_Activities_BivariateNormalExperiment | Estimate the equation of a line of best fit to make and test conjectures]]=== | ===[[SOCR_EduMaterials_Activities_BivariateNormalExperiment | Estimate the equation of a line of best fit to make and test conjectures]]=== | ||
| - | ===Interpret the slope and y-intercept of a line through data === | + | ===[[SOCR_EduMaterials_Activities_BivariateNormalExperiment | Interpret the slope and y-intercept of a line through data]]=== |
| - | ===Predict y-values for given x-values when appropriate using a line fitted to bivariate numerical data=== | + | ===[[SOCR_EduMaterials_Activities_BivariateNormalExperiment | Predict y-values for given x-values when appropriate using a line fitted to bivariate numerical data]]=== |
==References== | ==References== | ||
Current revision as of 21:28, 8 February 2008
SOCR May 2008 Event - Summarize, display, and analyze bivariate data
Collect, record, organize, and display a set of data with at least two variables
Use the Hot dog Sodium Calorie Dataset and explore various bivariate activities.
Determine whether the relationship between two variables is approximately linear or nonlinear by examination of a scatter plot
Characterize the relationship between two linear related variables as having positive, negative, or approximately zero correlation
Try scatter plotting the Weight or the Height (Y-axis) agains the index of the observation for the first 100 subjects in the Human Weight/Height Dataset. Of course, there should be no correlation between the index of the subject and his/her height or weight, as subjects are randomly chosen! On the contrary plotting Weight vs. height will demonstrate a clear positive correlation (i.e., higher weight implier taller individual).
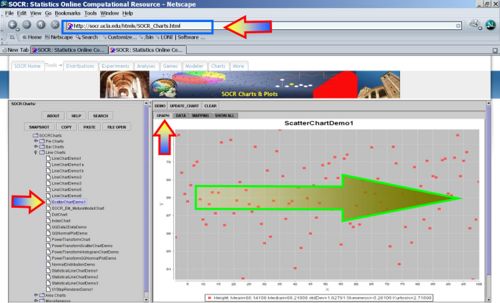
Estimate, interpret, and use lines fit to bivariate data
Estimate the equation of a line of best fit to make and test conjectures
Interpret the slope and y-intercept of a line through data
Predict y-values for given x-values when appropriate using a line fitted to bivariate numerical data
References
- Utah Secondary Core Curriculum Standards for Statistics
- Interactive Statistics Education EBook
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
