Simple Linear Regression Tutorial
From Socr
(Created page with '==SOCR_EduMaterials_AnalysesActivities - Simple Linear Regression Tutorial== '''Simple Linear Regression Tutorial Using LA Neighborhoods Data''' '''Data:''' We will be usin…') |
|||
| Line 10: | Line 10: | ||
''Step 2:'' Next, head to http://socr.ucla.edu/htmls/SOCR_Analyses.html, and find the Simple Regression Analysis Activity in the drop-down menu. [[File:SReg2.png|center|800px]] | ''Step 2:'' Next, head to http://socr.ucla.edu/htmls/SOCR_Analyses.html, and find the Simple Regression Analysis Activity in the drop-down menu. [[File:SReg2.png|center|800px]] | ||
| + | |||
| + | ''Step 3:'' Now Click the “PASTE” button under the drop down menu. You should now see the data in the window. [[File:SReg3.png|center|800px]] | ||
| + | |||
| + | ''Step 4:'' Click on the “MAPPING” tab, and add Income to the dependent variable list and Age to the independent variable list. [[File:SReg4.png|center|800px]] | ||
| + | |||
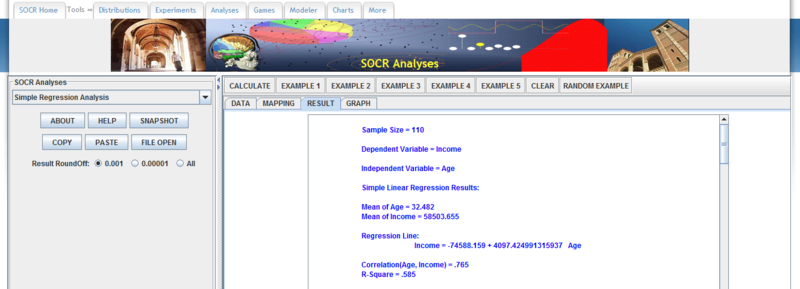
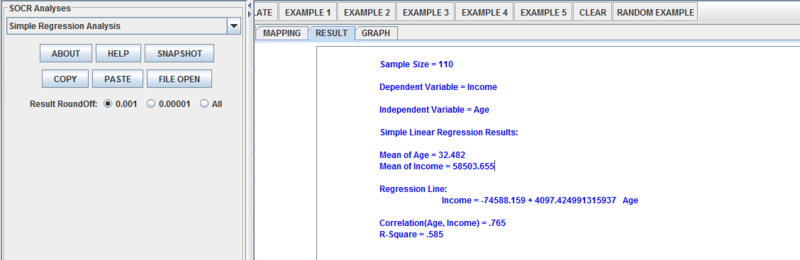
| + | ''Step 5:'' Click “CALCULATE”. You will now be taken to the “RESULTS” tab. [[File:SReg5.png|center|800px]] Here you can see the regression equation, <math>R^2</math>, individual residuals, and also mean and standard deviation for both variables. | ||
| + | |||
| + | |||
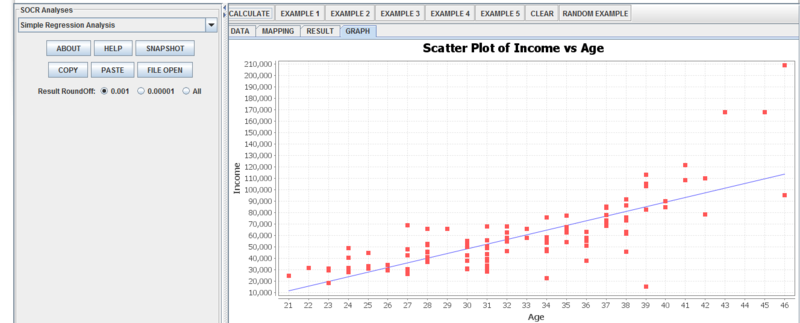
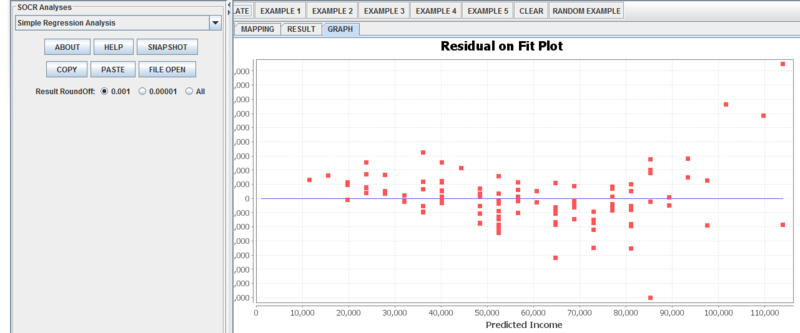
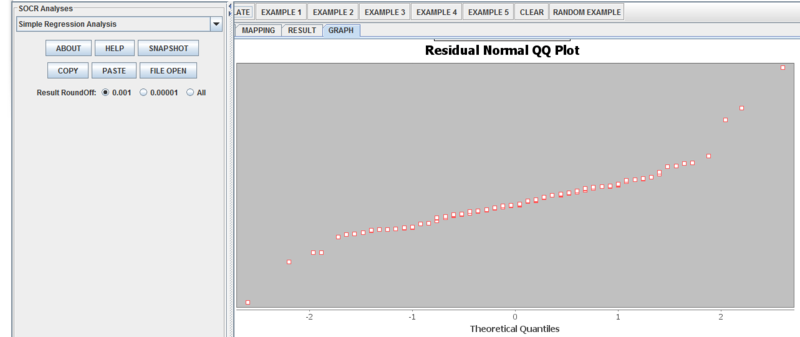
| + | ''Step 6:'' Click “GRAPH”. Here is the scatterplot of Income vs Age. We see the upward trend: As median age increases, so does median household income [[File:SReg6.png|center|800px]]. There are also residual plots [[File:SReg7.png|center|800px]]and the Normal-QQ Plot[[File:SReg8.png|center|800px]]. | ||
| + | |||
| + | ''Step 7:'' We want to check that the assumptions of linear regression, and make sure that they are met. | ||
| + | |||
| + | Assumption 1: There is a linear relationship between the independent (age) and dependent variable (income) | ||
| + | * How to check: Make a scatter plot of income and age | ||
| + | * How to fix: Transformations (for example Log(y) vs x), or the relationship is not linear. | ||
| + | '''''Assumption Met''''' | ||
| + | |||
| + | Assumption 2: The variance is constant | ||
| + | * How to check: Look at plot of residuals vs. predicted values ( ). Make sure there is not a pattern, such as the residuals getting larger as the predicted values increase. | ||
| + | * How to fix: Logging of variables, fixing underlying independence or linearity causes. | ||
| + | '''''Slight increase of residuals at the high end of age''''' | ||
| + | |||
| + | Assumption 3: Errors are normally distributed | ||
| + | * How to check: Normal QQ Plot (Should lie close to straight line) | ||
| + | * How to fix: Take out outliers, if applicable. Non-linear transformation may be needed | ||
| + | '''''Assumption Met''''' | ||
| + | |||
| + | '''Conclusions''' | ||
| + | |||
| + | No major violation of linear regression assumptions, we proceed with our analysis: | ||
| + | |||
| + | We can see from the results tab that the regression equation is: [[File:SReg9.png|center|800px]] | ||
| + | |||
| + | Income = -74549.596 + 4096.055 age | ||
| + | |||
| + | Income is the predicted value, -74549.596 is the intercept, 4096.055 is the slope, and age is the independent variable. | ||
| + | |||
| + | '''The linear model states that for every 1 year increase in median age, the median household income will increase by $4,096.06.''' | ||
Revision as of 06:58, 24 July 2011
SOCR_EduMaterials_AnalysesActivities - Simple Linear Regression Tutorial
Simple Linear Regression Tutorial Using LA Neighborhoods Data
Data: We will be using the LA Neighborhoods Data for this tutorial.
Goal: Our goal is to predict the median income using one explanatory variable by using SOCR. In this example, we will use the age variable.
Step 1: First, we will import the data into the SOCR Simple Regression Analysis Activity. Head to http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_LA_Neighborhoods_Data#Data_Source and find the table with the data. Select all of the data, and press Ctrl+C (Apple+C on Macs) to copy it.
Step 2: Next, head to http://socr.ucla.edu/htmls/SOCR_Analyses.html, and find the Simple Regression Analysis Activity in the drop-down menu. Step 3: Now Click the “PASTE” button under the drop down menu. You should now see the data in the window. Step 4: Click on the “MAPPING” tab, and add Income to the dependent variable list and Age to the independent variable list. Step 5: Click “CALCULATE”. You will now be taken to the “RESULTS” tab. Here you can see the regression equation, R2, individual residuals, and also mean and standard deviation for both variables.
Step 7: We want to check that the assumptions of linear regression, and make sure that they are met.
Assumption 1: There is a linear relationship between the independent (age) and dependent variable (income)
- How to check: Make a scatter plot of income and age
- How to fix: Transformations (for example Log(y) vs x), or the relationship is not linear.
Assumption Met
Assumption 2: The variance is constant
- How to check: Look at plot of residuals vs. predicted values ( ). Make sure there is not a pattern, such as the residuals getting larger as the predicted values increase.
- How to fix: Logging of variables, fixing underlying independence or linearity causes.
Slight increase of residuals at the high end of age
Assumption 3: Errors are normally distributed
- How to check: Normal QQ Plot (Should lie close to straight line)
- How to fix: Take out outliers, if applicable. Non-linear transformation may be needed
Assumption Met
Conclusions
No major violation of linear regression assumptions, we proceed with our analysis:
We can see from the results tab that the regression equation is:Income = -74549.596 + 4096.055 age
Income is the predicted value, -74549.596 is the intercept, 4096.055 is the slope, and age is the independent variable.
The linear model states that for every 1 year increase in median age, the median household income will increase by $4,096.06.