UQuadraticDistribuionAbout
From Socr
(Difference between revisions)
m (→Properties) |
m |
||
| Line 10: | Line 10: | ||
<center>(vertical scale) <math>\alpha = {12 \over \left ( b-a \right )^3}</math>. | <center>(vertical scale) <math>\alpha = {12 \over \left ( b-a \right )^3}</math>. | ||
</center> | </center> | ||
| - | + | More information about U-quadratic, and other continuous distribution functions, is available at [http://en.wikipedia.org/wiki/UQuadratic_distribution Wikipedia]. | |
===Properties=== | ===Properties=== | ||
Revision as of 20:32, 6 November 2007
Contents |
About_pages_for_SOCR_Distributions - U-Quadratic Distribution
Description
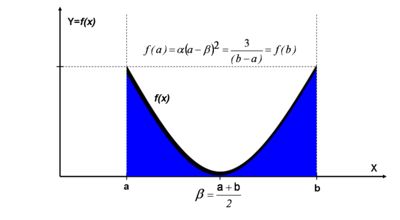
The U quadratic distribution is defined by the following density function
![f(x)=\alpha \left ( x - \beta \right )^2, \forall x \in [a , b], a < b](/socr/uploads/math/2/3/7/237b827942b590ee6636a63bd9d34231.png) ,
, where the relation between the two pairs of parameters (domain-support, a and b) and (range/offset α and β) are given by the following two equations
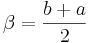 , and
, and
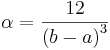 .
.
More information about U-quadratic, and other continuous distribution functions, is available at Wikipedia.
Properties
- Support Parameters:
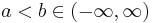
- Scale/Offset Parameters:
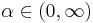 and
and 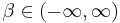
- PDF:
![f(x)=\alpha \left ( x - \beta \right )^2, \forall x \in [a , b]](/socr/uploads/math/0/e/c/0ec63e2753e9da97c974072666e6b00a.png)
- CDF
![F(x)={\alpha \over 3} \left ( (x - \beta)^3 + (\beta - a)^3 \right ), \forall x \in [a , b]](/socr/uploads/math/a/d/7/ad7a1289bc46726c7f54a39f7829d022.png)
- Mean:
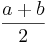
- Median:
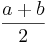
- Modes: a and b
- Variance:
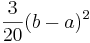
- Skewness: 0 (distribution is symmetric around the mean)
- Kurtosis:
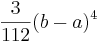
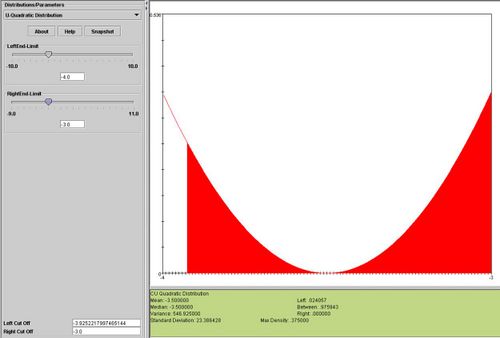
Interactive U Quadratic Distribution
You can see the interactive U Quadratic distribution by going to SOCR Distributions and selecting from the drop down list of distributions U Quadratic. Then follow the Help instructions to dynamically set parameters, compute critical and probability values using the mouse and keyboard.
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: