AP Statistics Curriculum 2007 EDA Center
From Socr
Contents |
General Advance-Placement (AP) Statistics Curriculum - Central Tendency
Measurements of Central Tendency
There are three main features of all populations (or data samples) that are always critical in understanding and interpreting their distributions. These characteristics are Center, Spread and Shape. The main measures of centrality are mean, median and mode.
Suppose we are interested in the long-jump performance of some students. We can carry an experiment by randomly selecting eight male statistics students and ask them to perform the standing long jump. In reality every student participated, but for the ease of calculations below we will focus on these eight students. The long jumps were as follows:
| 74 | 78 | 106 | 80 | 68 | 64 | 60 | 76 |
Mean
The sample-mean is the arithmetic average of a finite sample of numbers. For instance, the mean of the sample 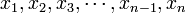 (short hand notation:
(short hand notation: 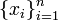 ), is given by:
), is given by:
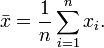
In the long-jump example, the sample-mean is calculated as follows:
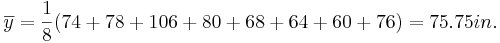
Median
The sample-median can be thought of as the point that divides a distribution in half (50/50). The following steps are used to find the sample-median:
- Arrange the data in ascending order
- If the sample size is odd, the median is the middle value of the ordered collection
- If the sample size is even, the median is the average of the middle two values in the ordered collection.
For the long-jump data above we have:
- Ordered data:
| 60 | 64 | 68 | 74 | 76 | 78 | 80 | 106 |
-
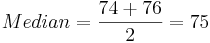 .
.
Mode(s)
The modes represent the most frequently occurring values (The numbers that appear the most). The term mode is applied both to probability distributions and to collections of experimental data.
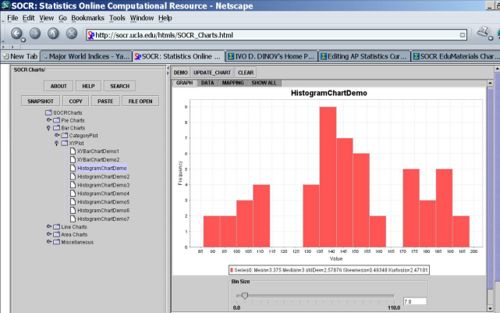
For instance, for the Hot dogs data file, there appears to be three modes for the calorie variable. This is presented by the histogram of the Calorie content of all hotdogs, shown in the image below. Note the clear separation of the calories into three distinct sub-populations - the highest points in these three sub-populations are the three modes for these data.
Resistance
A statistic is said to be resistant if the value of the statistic is relatively unchanged by changes in a small portion of the data. Referencing the formulas for the median, mean and mode which statistic seems to be more resistant?
If you remove the student with the long jump distance of 106 and recalculate the median and mean, which one is altered less (therefore is more resistant)? Notice that the mean is very sensitive to outliers and atypical observations, and hence less resistant than the median.
Resistant Mean-related Measures of Centrality
The following two sample measures of population centrality estimate resemble the calculations of the mean, however they are much more resistant to change in the presence of outliers.
K-times trimmed mean
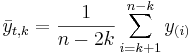 , where
, where 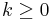 is the trim-factor (large k, yield less variant estimates of center), and y(i) are the order statistics (small to large). That is, we remove the smallest and the largest k observations from the sample, before we compute the arithmetic average.
is the trim-factor (large k, yield less variant estimates of center), and y(i) are the order statistics (small to large). That is, we remove the smallest and the largest k observations from the sample, before we compute the arithmetic average.
Winsorized k-times mean
The Winsorized k-times mean is defined similarly by 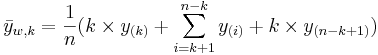 , where
, where 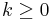 is the trim-factor and y(i) are the order statistics (small to large). In this case, before we compute the arithmetic average, we replace the k smallest and the k largest observations with the kth and (n-k)th largest observations, respectively.
is the trim-factor and y(i) are the order statistics (small to large). In this case, before we compute the arithmetic average, we replace the k smallest and the k largest observations with the kth and (n-k)th largest observations, respectively.
Other Centrality Measures
The arithmetic mean answers the question, if all observations were equal, what would that value (center) have to be in order to achieve the same total?
In some situations, there is a need to think of the average in different terms, not in terms of arithmetic average.
Harmonic Mean
If we study speeds (velocities) the arithmetic mean is inappropriate. However the harmonic mean (computed differently) gives the most intuitive answer to what the "middle" is for a process. The harmonic mean answers the question if all the observations were equal, what would that value have to be in order to achieve the same sample sum of reciprocals?
- Harmonic mean:
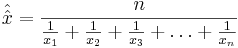
Geometric Mean
In contrast, the geometric mean answers the question if all the observations were equal, what would that value have to be in order to achieve the same sample product?
- Geometric mean:
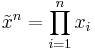
- Alternatively:
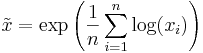
Medimean
We have already seen the standard definitions for mean and median. There is an alternative ways to define these measures of centrality using optimization theory.
- Median = \( argmin_x \big ( \sum_{s\in S} {|s-x|^1} \big )\)
- Mean = \( argmin_x \big ( \sum_{s\in S} {|s-x|^2}\big )\)
- where \( argmin_x \) provides the value x which minimizes the distance function in the operator.
The median and mean, as measures of centrality, represent points that are close to all the values randomly generated by the process. Thus, these parameters minimize the total sum of distances between them and each possible process observation, however, the differences between them is related to the differences in the metric used to compute distances between pairs of numbers.
For the mean, the expression above uses the squared Euclidean distance, \(L_2\) norm, which is procedurally different from the arithmetic averaging, or expectation calculation we have seen below, but generates the same result. The median optimization-based expression relies on the Manhattan distance, or \(L_1\) norm.
- The Medimean is a fusion of median and mean, (which is another word for average), which is defined by:
- Medimean(k) = \( argmin_x \big ( \sum_{s\in S} {|s-x|^k} \big )\)
The medimean depends on one parameter k, the distance exponent. For k=1, the medimean coincides with the median, and for k=2, it equals the mean. Thus, the medimean is a continuous and natural extension of the median and the mean for higher order exponents.
The medimean may be used as a compromise between the mean and the median. For example, if you are interested in something like a median, but which moves just a little bit in the direction of far-away elements, if there are any. In that case you may want to use a medimean(1.2) in the analysis.
How do we prove the equivalence of ht standard mean and median definitions and the optimization based definitions of these population parameters?
- For the Median = \( argmin_x \big ( \sum_{s\in S} {|s-x|^1} \big )\), this translates in the continuous variable case to \( argmin_x \big ( \int_{s\in S} {|s-x|^1P(x)dx} \big )\)=
- \( argmin_x \big ( \int_{s<m} {(m-s)P(s)ds} + \int_{s>m} {(m-s)P(s)ds} \big )\)=
- \( argmin_x \big ( m \int_{s<m} {P(s)ds} - \int_{s<m} {xP(s)ds} + m \int_{s>m} {P(s)ds} -\int_{s>m} {sP(s)ds} \big )\)=
- \( argmin_x \big ( m (F(m) -(1-F(m))) + \int_{s>m} {sP(s)ds} -\int_{s<m} {sP(s)ds} \big )\), where the cumulative distribution function \( F(m)= \int_{s<m} {P(s)ds} \).
- And this function, \( m (2F(m) -1) + \int_{s>m} {sP(s)ds} -\int_{s<m} {sP(s)ds}\), is minimized for \(m=F^{-1}(0.5)\), which is the standard definition of the median .
- For the Mean = \( argmin_x \big ( \sum_{s\in S} {|s-x|^2}\big )\), observe that minimizing \( \sum_{s\in S} {|s-x|^2}\) is similar to minimizing the variance of the process \( \sum_{s\in S} {(s-x)^2P(x)}\), which is identical to minimizing \(E(X^2)-\mu^2\), for \(\mu\).
Problems
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: