SOCR EduMaterials Activities MatchingExperiment
From Socr
Contents |
Matching Experiment
Description
Quite often, a method used to solve a problem in probability can be used to solve many other problems which at first glance appear different, but are conceptually the same. This exercise illustrates this situation using the SOCR Matching Experiment.
Goal
The aims of this activity are to demonstrate the concept of permutation. The matching experiment is to randomly permute n balls, numbered 1 to n. A match occurs whenever the ball number and the position number agree. The matches are shown in red. The number of matches N is recorded on each update. The distribution and moments of N are shown in the distribution graph and the distribution table. The parameter n can be varied with a scroll bar.
Experiment
Go to the SOCR Experiments and select the Matching Experiment from the drop-down list of experiments on the top left. The image below shows the initial view of this experiment:
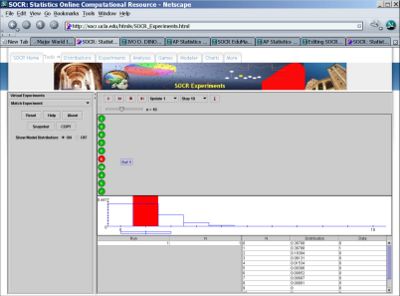
When pressing the play button, one trial will be executed and recorded in the distribution table below. The fast forward button runs larger number of trials. The stop button ceases any activity and is helpful when the experimenter chooses “continuous,” indicating an infinite number of events. The fourth button will reset the entire experiment, deleting all previous information and data collected. The “update” scroll indicates nth number of trials (1, 10, 100, or 1000) performed when selecting the fast forward button and the “stop” scroll indicates the maximum number of trials in the experiment.
Applications
Example 1
Six students are working on a project for their Statistics class that requires a lot of calculations. Each of them is in charge of calculating one part of the project, but they all will share the results. As they work, they pass around their papers so that everyone can see the results of the others. The smoke alarm sounds suddenly and each student grabs the nearest paper and hurriedly leaves the room. What is the theoretical probability that none of the students took his or her paper? What is the probability that you obtain from the data generated after repeating the correct experiment 1000 times?
- Attach a snapshot of the applet that shows how you found your answer with SOCR. The snapshot should show the theoretical true probability and the probability you got by repeating this experiment 1000 times. Highlight what in the snapshot is your answer.
Example 2
20 ladies arrive to a party and leave their coats with the concierge, who is not a very organized person. At the end of the party, the ladies don’t really remember what their coats look like (too much dancing and chocolate cake) and have lost the numbers the concierge gave them. So the concierge has to give them the coats back at random. What is the theoretical probability that at least two ladies get their own coat? What is the probability that you obtain from the data generated after repeating the correct experiment 1000 times?
- Attach a snapshot of the applet that shows how you found your answer with SOCR. The snapshot should show the theoretical true probability and the probability you got by repeating (appropriately) this experiment 1000 times. Highlight what in the snapshot is your answer.
Translate this page:
