SOCR EduMaterials Activities ProportionTestExperiment
From Socr
Contents |
Proportion Test Experiment
Description
The experiment is to select a random sample of size n from the Bernoulli distribution with parameter p, and then to construct and approximate confidence interval for p at a specified confidence level. The true value of p can be varied with a scroll bar. The density of the Bernoulli distribution and the value of p are shown in blue in the first graph.
The confidence level can be selected from a list box, as well as the type of interval – two sided, upper bound, or lower bound. The interval is constructed using quantities from the standard normal distribution. The standard normal density and the critical values are shown in blue in the second graph.
Variables L and R denote the left and right endpoints of the confidence interval and I indicates the event that the confidence interval contains p. The theoretical density of I is shown in blue in the third graph.
On each update, the sample density and the confidence interval are shown in red in the first graph, and the computed standard score is shown in red in the second graph. Note that the confidence interval contains p in the first graph if and only if the standard score falls between the critical values in the second graph. The third graph shows the proportion of successes and failures in red. The first table gives the sample values; the second table records L, R, the standard score Z, and I. Finally, the third table gives the theoretical and empirical densities of I.
Goal
The purpose is to provide a simulation that provides data from the Bernoulli distribution that allows others to develop a better understanding of confidence intervals numerically and graphically. It will give them the advantage to develop their own generalizations regarding proportion estimates and theoretical tests.
Experiment
Go to the SOCR Experiment and select the Proportion Test Experiment from the drop-down list of experiments on the top left. The image below shows the initial view of this experiment:
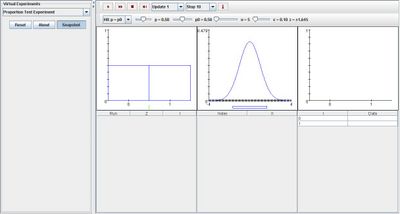
When pressing the play button, one trial will be executed and recorded in the distribution table below. The fast forward button symbolizes the nth number of trials to be executed each time. The stop button ceases any activity and is helpful when the experimenter chooses “continuous,” indicating an infinite number of events. The fourth button will reset the entire experiment, deleting all previous information and data collected.
The “update” scroll indicates nth number of trials (1, 10, 100, or 1000) performed when selecting the fast forward button and the “stop” scroll indicates the maximum number of trials in the experiment.
Initially, the experiment sets p = p0 as the null hypothesis in the list box. When varying parameter p, increasing p will raise the proportion of value 1 in the distribution graph of the first image and decreasing p will lower the proportion of value 0. The changes in the first image will occur for all selections of the null hypothesis in the list box. Similarly, when modifying p0, the green indicator in the first graph will shift accordingly.
As for parameter alpha, the second graph will vary. The indicating box under the graph will shift to the right as alpha is increased and shift to the left when alpha is decreased. But the indicating box will be centered uniquely for all selections of the null hypothesis. When selecting p = p0, the box will be centered in the middle of the graph. For p greater than or equal to p0, the box will be centered toward the right side of the graph and for p less than or equal to p0, the box will be centered toward the left side of the graph.
The image shown below demonstrates these properties when selecting p is greater than or equal to p0 with a large alpha value:
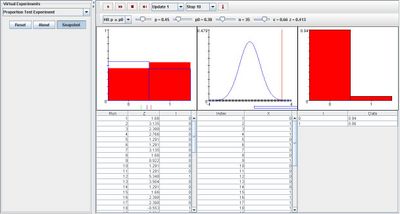
As trials are executed, the empirical density graph converges toward the distribution graphs of the first and third graphs. Also note that parameter alpha affects the outcome of the third graph. With a large value of alpha, the proportion of value 1 in the third graph obtains a higher value. The image below demonstrates this:
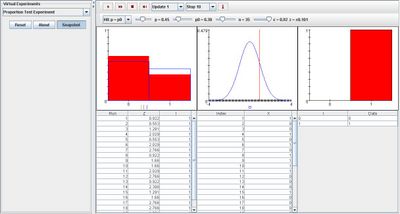
Applications
The Proportion Test Experiment is a simple simulation that demonstrates the outcomes of Bernoulli trials with successes and failures. It may be used in many different types of situations such as:
Suppose stock brokers want to test the proportions of successes and failures of a specific identified company.
Suppose researchers want to illustrate their findings of successes and failures of an enhanced pain killer.
Translate this page:
