SOCR EduMaterials Activities SampleMeanExperiment
From Socr
Contents |
Sample Mean Experiment
Description
The applet is part of the SOCR Experiments: Sampling Distribution (CLT) Experiment, which demonstrates the properties of the sampling distributions of various sample statistics. This applet can be used to demonstrate the Central Limit Theorem (CLT) as well as:
1. Investigate the effect of the Native population on various sample statistics 2. Study the effects of the sample-sizes on the sampling distribution 3. Determine which sample statistics may have known distributions (e.g. Normal), under what conditions 4. Explore the relations between Population parameters and their corresponding sample counterparts. For example, population mean/SD and sample mean/SD, symmetry, distribution shape, etc.
Goal
The main focus of the Sample Mean Experiment is to provide a simple simulation of four sampling distributions: normal, gamma, binomial, and Poisson. After using this Java applet, one should have a better understanding of the different types of distribution and have the ability to develop a generalization regarding these allocations.
Experiment
Go to the SOCR Experiment [SOCR Experiment] and select the Sample Mean Experiment from the drop-down list of experiments on the top left. The image below shows the initial view of this experiment:
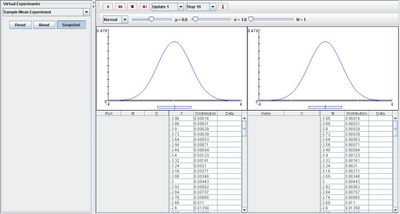
When pressing the play button, one trial will be executed and recorded in the distribution table below. The fast forward button symbolizes the nth number of trials to be executed each time. The stop button ceases any activity and is helpful when the experimenter chooses “continuous,” indicating an infinite number of events. The fourth button will reset the entire experiment, deleting all previous information and data collected. The “update” scroll indicates nth number of trials (1, 10, 100, or 1000) performed when selecting the fast forward button and the “stop” scroll indicates the maximum number of trials in the experiment.
Normal
When varying the parameters, both distribution graphs are not effects graphically; they remain normal. The image below demonstrates this after many trials:
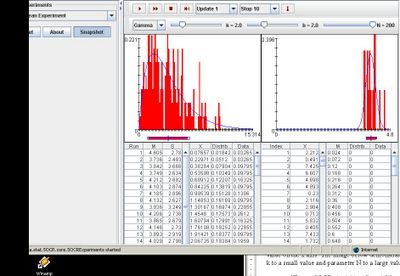
Gamma
Varying parameter k shifts both graphs to the right. Modifying parameter N also affects the distribution graph on the right as it decreases the spread by increasing the smallest value on the x axis. The image below demonstrates these properties by setting parameter k to a small value and parameter N to a large value:
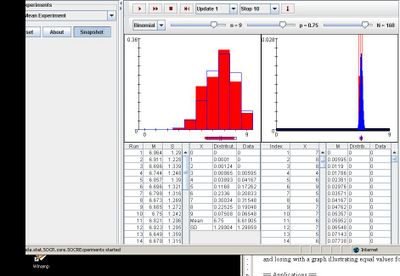
Binomial
In order for data to be represented more accurately, increasing parameter n will cause the shapes of the two distribution graphs to be more curved which will demonstrate better values for the experiment. Increasing p shifts both graphs to the right and decreasing p shifts both graphs to the left. Lastly, increasing parameter N only creates a more accurate distribution graph on the right and decreasing parameter N makes the graph less precise. The image below illustrates a binomial distribution with a large sample size n, large parameter p, and large size of N:
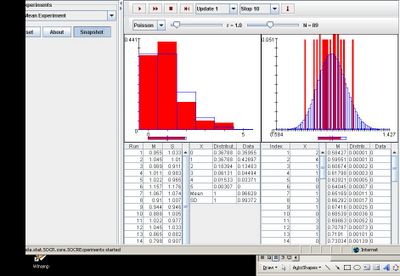
Poisson
Similar to the rest of the distributions, modifying parameter N only affects the distribution graph on the right. When varying parameter r, both graphs are changed as increasing the parameter will cause the graphs to become more curved, and decreasing the parameter will cause the graphs to become less curved. The image below demonstrates these characteristics:
Applications
The Sample Mean Experiment is a simple application that can be used in many different types of situations such as:
Suppose researchers want to be able to display their research findings. While selecting 50 adults from a building, they found that the probability of people in their specified age range drinking coffee every morning is approximately normal. Using this applet gives them the ability to do so.
Suppose students want to be able to demonstrate their data information from their science labs. They discovered the probability of rain in a given day and chose specified weeks in the year as their sample mean. By using this applet, they are able to vary the parameters and illustrate their findings.
Translate this page:
