SOCR EduMaterials Activities TriangleExperiment
From Socr
Contents |
Triangle Experiment
Description
Two points are chosen at random in the interval [0, 1]; X denotes the first point chosen and Y denotes the second point chosen. Random variable U gives the type of triangle that can be formed from the three sub-intervals: U = 0, the pieces do not form a triangle; U = 1, the pieces form an obtuse triangle; U = 2, the pieces form an acute triangle. The first picture box shows the outcome of the experiment graphically. On each update, the cut points X and Y are shown as red dots, and the triangle is sketched when U = 1 or U = 2. The second picture box shows the sample space and the three events of interest: U = 2 consists of the 2 interior regions; U =1 consists of the 6 middle regions; U = 0 consists of the outer regions. On each run, (X, Y) is shown as a red dot in the scatter plot, and is recorded in the first table on each update. The probability density function of U is shown in blue in the graph box and is recorded in the graph table. On each update, the empirical density of U is shown in red in the graph box and is recorded in the graph table. Additionally, the value of U is recorded in the first table on each update.
Goal
The main focus of the Triangle Experiment is to provide a simulation that demonstrates graphically and analytically of random points forming triangles. After using this applet, users should be able to understand the properties and characteristics of calculus based probability.
Experiment
Go to the SOCR Experiment [SOCR Experiment] and select the Triangle Experiment from the drop-down list of experiments on the top left. The image below shows the initial view of this experiment:
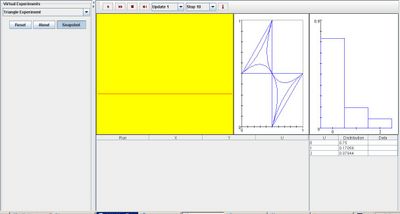
When pressing the play button, one trial will be executed and recorded in the distribution table below. The fast forward button symbolizes the nth number of trials to be executed each time. The stop button ceases any activity and is helpful when the experimenter chooses “continuous,” indicating an infinite number of events. The fourth button will reset the entire experiment, deleting all previous information and data collected. The “update” scroll indicates nth number of trials (1, 10, 100, or 1000) performed when selecting the fast forward button and the “stop” scroll indicates the maximum number of trials in the experiment.
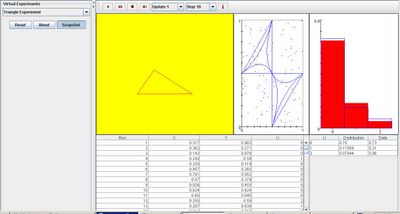
As the number of trials increase, the empirical density graph converges to the distribution graph on the right. The scatter plot keeps record of every run and the triangle on the left must be changed after every run to illustrate the type of shape formed. The image below demonstrates this:
Applications
The Triangle Experiment is a simple application that can be used in calculus based probability events. It may also be used in real life situations such as:
Suppose entry-level architectures want to determine the probability of randomly selecting points to form an equilateral triangle. After using this applet, they are able to analytically and geometrically demonstrate that the probability for the event of interest to occur is very small.
Suppose constructors are given an area in which they can plot 12 points total and form the basis of a building that are shaped as triangles. By using this applet, they are able to explore the many different types and shapes of triangles that can be formed under these conditions.
Translate this page:
