SOCR EduMaterials Activities VarianceEstimateExperiment
From Socr
Contents |
Variance Estimate Experiment
Description
The experiment is to select a random sample of size n from a specified distribution, and then to construct an approximate confidence interval for σ at a specified confidence level. The distribution can be chosen with a list box; the options are N(μ,σ2), Γ, and uniform. In each case, the appropriate parameters and the sample size can be varied with scroll bars. The density, μ, and σ of the selected distribution are shown in blue in the first graph. The confidence level can be selected from a list box, as can the type of interval--two sided, upper bound, or lower bound. The interval can be constructed assuming either that the distribution mean μ is known or unknown. In the first case the pivot variable V has the χ2 distribution with n degrees of freedom; in the second case the pivot variable V has χ2 distribution with n - 1 degrees of freedom. The density and the critical values of V are shown in blue in the second graph. Variables L and R denote the left and right endpoints of the confidence interval and I indicates the event that the confidence interval contains the distribution mean. The theoretical density of I is shown in blue in the third graph. On each update, the sample density and the confidence interval are shown in red in the first graph, and the value of V is shown in red in the second graph. Note that the confidence interval contains the mean in the first graph if and only if V falls between the critical values in the second graph. The third graph shows the proportion of successes and failures in red. The first table gives the sample values; the second table records L, R, V, and I. Finally, the third table gives the theoretical and empirical densities of I.
Goal
The purpose of the Variance Estimate Experiment is to provide a simple simulation of approximating confidence intervals for the selected list of distributions. After using this Java applet, one should have a better understanding regarding events dealing with chi square estimate, gamma, and uniform distributions.
Experiment
Go to the SOCR Experiment [SOCR Experiment] and select the Variance Estimate Experiment from the drop-down list of experiments on the top left. The image below shows the initial view of this experiment:
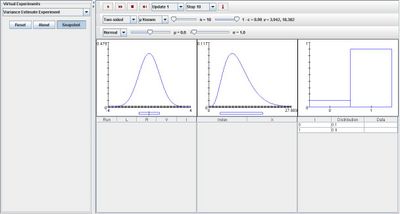
When pressing the play button, one trial will be executed and recorded in the distribution table below. The fast forward button symbolizes the nth number of trials to be executed each time. The stop button ceases any activity and is helpful when the experimenter chooses “continuous,” indicating an infinite number of events. The fourth button will reset the entire experiment, deleting all previous information and data collected. The “update” scroll indicates nth number of trials (1, 10, 100, or 1000) performed when selecting the fast forward button and the “stop” scroll indicates the maximum number of trials in the experiment.
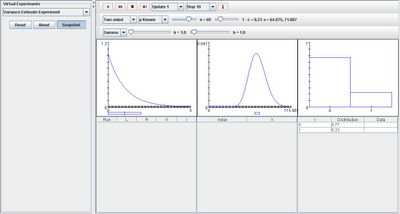
Modifying parameters n and 1-alpha affects the shapes of the distribution graph in the middle and the image on the right. Increasing 1-alpha increases the proportion for 1 in the last image and decreasing it increases the proportion for 0. Increasing parameter n shifts the left end point of the middle graph to the right, resulting in a smaller value of spread. The image below demonstrates these two properties:
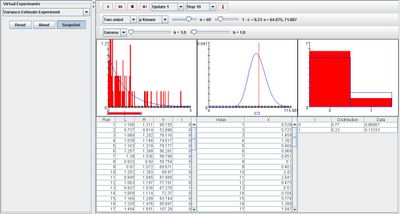
As the number of trials increase, the empirical density graph converges to the distribution graphs for the first and last images displayed. The image below demonstrates this:
Applications
The Variance Estimate Experiment is a simple application that can be used in many different types of situations such as:
Suppose students need to present their experiment of selecting a pack of 24 cans of soda to measure the mean and standard deviation of weight. Once all the information has been gathered and analyzed, using this application can help display their conclusion easily.
Suppose engineers want to display data information regarding the average weight in metal bars in their industry. Because measuring every single bar in the company is impossible, the engineers decide to use this application by selecting “Mean unknown” in one of the list boxes and run the experiment a few times until the resulting images satisfy the requirements.
Translate this page:
