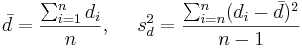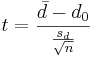SOCR EduMaterials AnalysisActivities TwoPairedT
From Socr
Contents |
SOCR Analysis - Two Paired Sample T-Test Example
This is a test for the hypothesis that two groups are with the same mean, while the data are actually paired. That is, Each value of group 1 has a corresponding value in group 2.
Two Paired Sample T-Test Example
Go to the SOCR Two Paired Sample T-Test Applet. We will demonstrate Two Paired T-Test with a SOCR built-in example. This example is based on a dataset from the statistical program "R." For more information of the R program, please see CRAN Home Page. The dataset used here is "shoes" under R's "MASS" library. In the dataset, ten boys are given to the wear of shoes of materials A and B for one foot. We'd like to find if one material is better than the other.
Here's the steps of the activity:
1. Click on Two Paired Sample T-Test at the left panel's combo box.
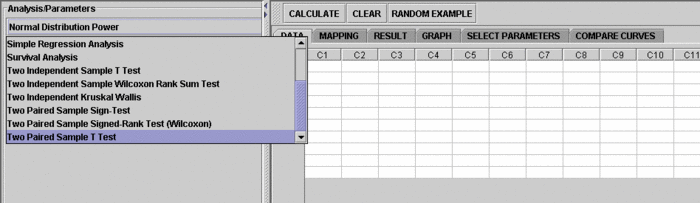
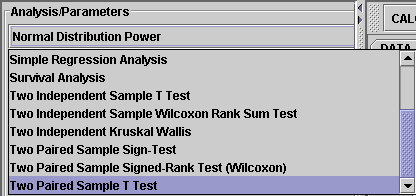
On the right panel, first click on EXAMPLE 3 and next click on "Data" to retreive the demonstrated example. This is the example we'll be looking at.Note that the data are difference of B - A.
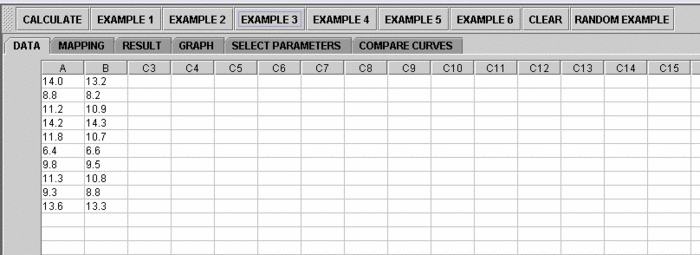
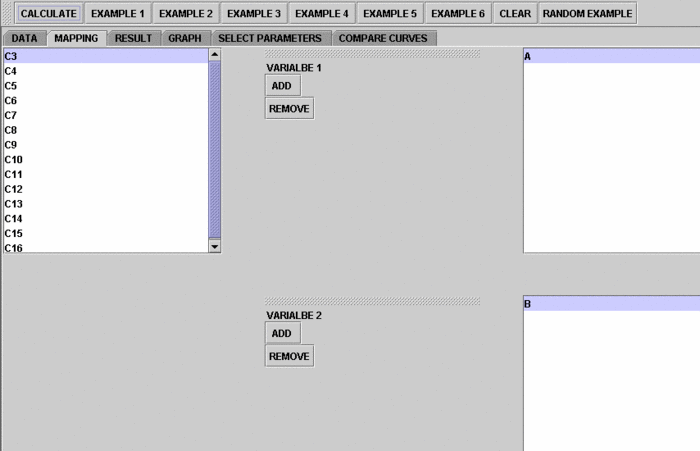
2. Click on the "Mapping" button to get to the "Mapping" panel. Click on "ADD" under VARIABLE 1 to add A and click on ADD under VARIABLE 2 to add B. We care about the difference, so which on goes to VARIABLE 1 or VARIABLE 2 is arbitrary. Here, the computer will set difference = Variable 2 - Variable 1. If you like the subtraction to go the other way around, simple assign VARIABLE 1 and VARIABLE 2 in the opposite way.
3. Click on "Calculate" then "Result" to see the results.

Questions for students: By looking at the test results, what do you think about the data? What can you say about the two different shoe materials?
Example 2
In many experiments the same variable is measured under two different conditions. For example, in clinical trials the participants may be evaluated at baseline and then evaluated again at the end of the treatment. For example, the blood pressure is measured for several patients before and after administration of certain drug. The difference between the value at baseline and the value at the end is computed for each participant as follows:
| Value at baseline | Value at the end | Difference | |
|---|---|---|---|
| Subject 1 | x1b | x1a | d1 = x1b − x1a |
| Subject 2 | x2b | x2a | d2 = x2b − x2a |
| Subject 3 | x3b | x3a | d3 = x3b − x3a |
| ... | ... | ... | ... |
| ... | ... | ... | ... |
| Subject n | xnb | xna | dn = xnb − xna |
We then compute the sample mean and sample standard deviation of the differences.
The hypothesis we want to test is: H0:μd = d0 vs. Ha:μd < d0 or μd > d0 or 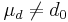 .
.
If we choose d0 = 0 we are testing whether the before and after treatment are the same.
- Test statistic:
- Assumption:
- The differences are treated as a random sample from a normal distribution.
We reject H0 if the t value falls in the rejection region which is based on the significance level α and n − 1 degrees of freedom.
To study the effect of cigarette smoking on platelet aggregation researchers drew blood samples from 11 individuals before and after they smoked a cigarette and measured the percentage of blood platelet aggregation (from Mathematical Statistics and Data Analysis, John Rice, Third Edition, Duxbury, 2007). Platelets are involved in the formation of blood clots, and it is known that smokers suffer more from disorders involving blood clots than do nonsmokers. This study can be found in Levine, P. H. (1973). An acute effect of cigarette smoking on platelet function, Circulation, 48, 619-623.
| Before | After | Difference |
|---|---|---|
| 25 | 27 | 2 |
| 25 | 29 | 4 |
| 27 | 37 | 10 |
| 44 | 56 | 12 |
| 30 | 46 | 16 |
| 67 | 82 | 15 |
| 53 | 57 | 4 |
| 53 | 80 | 27 |
| 52 | 61 | 9 |
| 60 | 59 | -1 |
| 28 | 43 | 15 |
- Test the null hypothesis that the means before and after are the same. Use α = 0.05.
References
Translate this page: