SOCR EduMaterials FunctorActivities Bernoulli Distributions
From Socr
This is an activity to explore the Moment Generating Functions for the Bernoulli, Binomial, Geometric and Negative-Binomial Distributions.
- Description: You can access the applets for the above distributions at http://www.socr.ucla.edu/htmls/SOCR_DistributionFunctors.html .
- Exercise 1: Use SOCR to graph the MGF's and print the following distributions and answer the questions below. Also, comment on the shape of each one of these distributions:
- a.
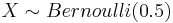
- b.
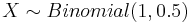
- c.
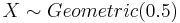
- d.
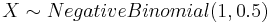
- a.
Below you can see a snapshot of the MGF of the distribution of 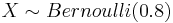
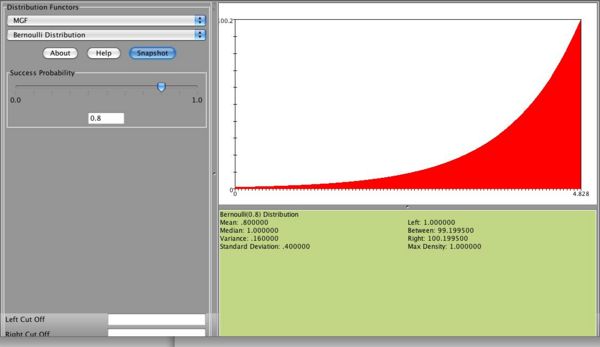
Do you notice any similarities between the graphs of these MGF's between any of these distributions?
- Exercise 2: Use SOCR to graph and print the MGF of the distribution of a geometric random variable with p = 0.2,p = 0.7. What is the shape of this function? What happens when p is large? What happens when p is small?
- Exercise 3: You learned in class about the properties of MGF's If X1,...Xn are iid. and
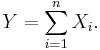 then
then ![M_{y}(t) = {[M_{X_1}(t)]}^n](/socr/uploads/math/2/1/7/217410c286efabe001a50f7198167f5d.png) .
.
- a. Show that the MGF of the sum of n independent Bernoulli Trials with success probability p is the same as the MGF of the Binomial Distribution using the corollary above.
- b. Show that the MGF of the sum of n independent Geometric Random Variables with success probability p is the same as the MGF of the Negative-Binomial Distribution using the corollary above.
- c. How does this relate to Exercise 1? Does having the same MGF mean they are distributed the same?
- Exercise 4: Graph the PDF and the MGF for the appropriate Distribution where
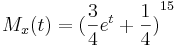 . Be sure to include the correct parameters for this distribution, for example if
. Be sure to include the correct parameters for this distribution, for example if 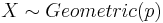 be sure to include the numeric value for p
be sure to include the numeric value for p
See also
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
