SOCR Events May2008 C3 S1
From Socr
SOCR May 2008 Event - Calculate probabilities of events and compare theoretical and experimental probability
Solve counting problems using the Fundamental Counting Principle
Suppose that a task involves a sequence of k choices. Let n1 be the number of ways the 1st stage or event can occur and n2 be the number of ways the 2nd stage or event can occur after the first stage has occurred. Continuing in this way, let be the number of ways the knd stage or event can occur after the first k - 1 stages or events have occurred. Then the total number of different ways the task can occur is: 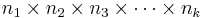 .
.
- Example: A deli has a lunch special which consists of a sandwich, soup, dessert and drink for $4.99. If they offer the following choices, how many lunch specials are possible?
- Sandwich: chicken salad, ham, and tuna, and roast beef
- Soup: tomato, chicken noodle, vegetable
- Dessert: cookie and pie
- Drink: tea, coffee, coke, diet coke and sprite
We can use the basic counting principle:
There are k=4 stages or events: choosing a sandwich, choosing a soup, choosing a dessert and choosing a drink. There are 4 choices for the sandwich, 3 choices for the soup, 2 choices for the dessert and 5 choices for the drink. Putting that all together we get:
Number of choices = 4 (sandwiches) x 3 (soups) x 2 (desserts) x 5 (drinks) = 120. So there are exactly 120 lunch specials possible at this deli.
Calculate the probability of an event or sequence of events with and without replacement using models
The Ball and Urn Experiment demonstrates the effects of sampling with or without replacement. Suppose we choose n balls at random from an urn containing R are red and (N-R) are green balls. For every trial, the number of red balls drawn (Y) are recorded numerically in the distribution table (on the right) and graphically in the distribution graph (blue). At each trial, the empirical frequency of Y is displayed in red the distribution graph. The experimenter has the abilities to manipulate trials by choosing with replacement or without replacement in the list box and varying parameters N, R, and n with scroll bars.
- Why is there a difference in sampling balls from the urn with or without replacement?
- Set N=50, R=25 and n=2. If you sample with replacement, what is the chance that we get 2 red balls in the sample of 2?
- If we sample without replacement and the first ball is red, what is the chance that the second ball will be also red? Is this probability effected by knowing the collor of the first drawn ball?
- If we increase or decrease R (number of red balls in the urn), how is the probability of drawing a red ball changing? Notice how the distribution (blue graph) becomes left- or right-skewed.
Recognize that the sum of the probability of an event and the probability of its complement is equal to one
For the Ball and Urn Experiment above, let E={Event that a sample of 2 balls contain at least one Red ball}. If N=50, R=25 and n=2 and we sample with replacement, what is the complement of this event, Ec? That are the probabilities of E and Ec? Does P(E) + P(Ec)=1? Is this expected?
Make approximate predictions using theoretical probability and proportions
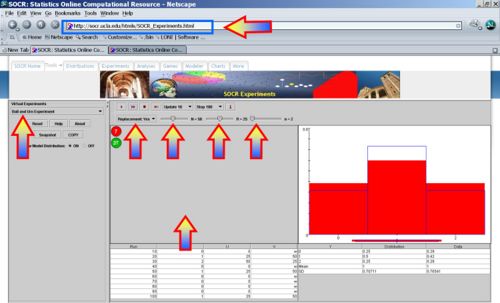
Suppose we did not know the values of R (real number of red balls in the urn) and we wanted to estimate R from a sample of 20 balls randomly chosen with replacement. How can we do that and what is the appropriate estimate for R? Note that each time you run this experiment, this estimate will slightly vary as this is a random experiment where chance plays role.
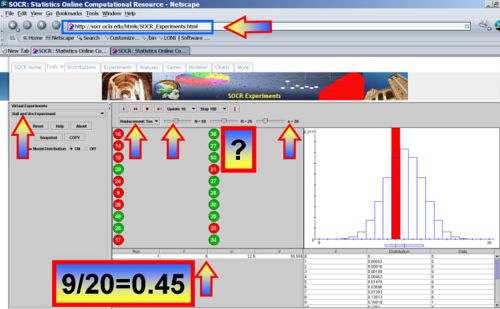
Collect and interpret data to show that as the number of trials increases, experimental probability approaches the theoretical probability
Increase the number of experiments to 1,000 and click the Run button. Notice hos the empirical peobabilities (red graph) quickly approach the theioretical probabilities (blue graph) and similarrly the theoretical and empirical probabilities become numerically similar (see bottom-right table).
References
- Utah Secondary Core Curriculum Standards for Statistics
- Interactive Statistics Education EBook
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
