AP Statistics Curriculum 2007 Distrib MeanVar
From Socr
(→Properties of Variance: added var(X) = E(X^2) - (EX)^2) |
(→Example) |
||
| Line 3: | Line 3: | ||
=== Expectation (Mean)=== | === Expectation (Mean)=== | ||
==== Example==== | ==== Example==== | ||
| - | Suppose 10% of the human population carries the green-eye allele. If we choose 1,000 people randomly and let the RV X be the number of green-eyed people in the sample. Then the distribution of X is binomial distribution with n = 1,000 and p = 0.1 (denoted as <math>X \sim B(1,000, 0.1)</math>. In a sample of 1,000 people, how many are we expecting to have this allele? Clearly the count of individuals that carry the green-eye allele will vary between different samples of 1,000 subjects. Well, now much dispersion between the samples can we expect, in terms of the number of individuals carrying this allele? These questions will be answered by computing the mean and the variance (or standard deviation) for this process. | + | Suppose 10% of the human population carries the green-eye allele. If we choose 1,000 people randomly and let the RV X be the number of green-eyed people in the sample. Then the distribution of X is binomial distribution with n = 1,000 and p = 0.1 (denoted as <math>X \sim B(1,000, 0.1)</math>. In a sample of 1,000 people, how many of them are we expecting to have this allele? Clearly the count of individuals that carry the green-eye allele will vary between different samples of 1,000 subjects. Well, now much dispersion between the samples can we expect, in terms of the number of individuals carrying this allele? These questions will be answered by computing the mean and the variance (or standard deviation) for this process. |
====Definition==== | ====Definition==== | ||
Revision as of 19:32, 28 June 2010
Contents |
General Advance-Placement (AP) Statistics Curriculum - Expectation (Mean) and Variance
Expectation (Mean)
Example
Suppose 10% of the human population carries the green-eye allele. If we choose 1,000 people randomly and let the RV X be the number of green-eyed people in the sample. Then the distribution of X is binomial distribution with n = 1,000 and p = 0.1 (denoted as 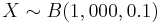 . In a sample of 1,000 people, how many of them are we expecting to have this allele? Clearly the count of individuals that carry the green-eye allele will vary between different samples of 1,000 subjects. Well, now much dispersion between the samples can we expect, in terms of the number of individuals carrying this allele? These questions will be answered by computing the mean and the variance (or standard deviation) for this process.
. In a sample of 1,000 people, how many of them are we expecting to have this allele? Clearly the count of individuals that carry the green-eye allele will vary between different samples of 1,000 subjects. Well, now much dispersion between the samples can we expect, in terms of the number of individuals carrying this allele? These questions will be answered by computing the mean and the variance (or standard deviation) for this process.
Definition
The Expected Value, Expectation or Mean, of a discrete random variable X is defined by| E[X] = | ∑ | xP(X = x). |
| x |
The expectation of a continuously-values random variable Y is analogously defined by ![E[Y]=\int{yP(y)dy}](/socr/uploads/math/3/5/3/35333821441a3f97afd34522524699d1.png) , where the integral is over the domain of Y and P(y) is the probability density function of Y.
, where the integral is over the domain of Y and P(y) is the probability density function of Y.
Properties of Expectation
- Expectation is a linear functional. That is, the expected value operator
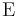 is linear in the sense that
is linear in the sense that

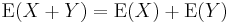

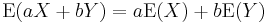 for any two random variables X and Y (which need to be defined on the same probability space) and any real numbers a and b. This property follows directly from the definition of expectation. For instance,
for any two random variables X and Y (which need to be defined on the same probability space) and any real numbers a and b. This property follows directly from the definition of expectation. For instance,
![E[aX+b]=\sum_x{(a\times x+b)P(X=x)} =
\sum_x{(a\times x)P(X=x)} +\sum_x{bP(X=x)} =](/socr/uploads/math/a/e/7/ae7d14a45b834d976e9b7eb61c1097a7.png)
![=a\times \sum_x{xP(X=x)} + b\times \sum_x{P(X=x)} =
a\times E[X] + b\times 1 =aE[X] + b.](/socr/uploads/math/c/4/7/c475fd2e7bc9edc922894c424e88f0a1.png)
-
![E[g(X)] = \sum_x{g(x)\times P(X=x)},](/socr/uploads/math/7/d/0/7d0b8656da37fd04a3feaba2fd5e6279.png) where g(x) is any real-valued function.
where g(x) is any real-valued function.
Variance
The Variance, of a discrete random variable X is defined by| VAR[X] = | ∑ | (x − E[X])2P(X = x). |
| x |
![VAR[Y]=\int{(y-E[Y])^2P(y)dy}](/socr/uploads/math/9/6/3/963de9de0b6bf18151bdd4f34b03ba48.png) , where the integral is over the domain of Y and P(y) is the probability density function of Y.
, where the integral is over the domain of Y and P(y) is the probability density function of Y.
Properties of Variance
- The Variance is not quite a linear functional. It has the following properties:
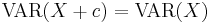 (Data shifts do not affect the dispersion.)
(Data shifts do not affect the dispersion.)
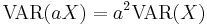
- If X and Y are uncorrelated,
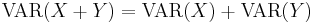
- If X and Y are dependent (correlated),
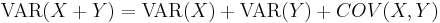
- An alternative formula for calculating the variance is: VAR(X) = E(X2) − (E(X))2.
- The Covariance between two real-valued random variables X and Y, with corresponding expected values
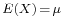 and
and 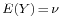 is defined as
is defined as
- In general, if we have {
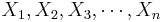 } correlated variables, then the variance of their sum is the sum of their covariances:
} correlated variables, then the variance of their sum is the sum of their covariances:
Standard Deviation
The Standard Deviation, of a discrete random variable X is defined by ![SD[X]=\sqrt{\sum_x{(x-E[X])^2P(X=x)}} = \sqrt{VAR[X]}.](/socr/uploads/math/6/3/e/63efcc8f9e290eca120d53ac0211ef6e.png) The standard deviation of a continuously-values random variable Y is analogously defined by
The standard deviation of a continuously-values random variable Y is analogously defined by ![SD[Y]=\sqrt{\int{(y-E[Y])^2P(y)dy}} = \sqrt{VAR[Y]}](/socr/uploads/math/d/3/c/d3c9979ffda69d44917d36856398702b.png) , where the integral is over the domain of Y and P(y) is the probability density function of Y.
, where the integral is over the domain of Y and P(y) is the probability density function of Y.
Higher Moments
Raw Moments
The kth Raw Moment for a discrete random variable X is defined by| E[Xk] = | ∑ | xkP(X = x). |
| x |
![E[Y^k]=\int{y^kP(y)dy},](/socr/uploads/math/1/b/0/1b0276799e29d88e58517f36b4ee7506.png) where the integral is over the domain of Y and P(y) is the probability density function of Y.
where the integral is over the domain of Y and P(y) is the probability density function of Y.
Centralized Moments
The kth Centralized Moment for a discrete random variable X is defined by| Ec[Xk] = | ∑ | (x − μ)kP(X = x), |
| x |
![E_c[Y^k]=\int{(y-\mu)^kP(y)dy},](/socr/uploads/math/0/0/7/00707fca33eb89717efcd84364a75654.png) where μ is the expected value of Y, the integral is over the domain of Y and P(y) is the probability density function of Y.
where μ is the expected value of Y, the integral is over the domain of Y and P(y) is the probability density function of Y.
Standardized Moments
The kth Standardized Moment for a discrete random variable X is defined by
The kth Standardized Moment for a continuously-values random variable Y is analogously defined by
![E_s[Y^k]={\int{(y-\mu)^kP(y)dy} \over \sigma^k},](/socr/uploads/math/d/f/d/dfd27aef870d59af11c6b2ed852867a0.png) where the integral is over the domain of Y and P(y) is the probability density function of Y
where the integral is over the domain of Y and P(y) is the probability density function of Y
Notable Moments
In addition to the mean and variance, the Skewness and the Kurtosis are two notable (3-rd and 4-th) moments, respectively.
Sample Moments
Sample Moments are, of course, analogously computed to their theoretical counterparts, using a sample of observations {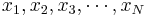 }. For example, the sample skewness and kurtosis (the 3-rd and 4-th sample standardized moments) are defined by
}. For example, the sample skewness and kurtosis (the 3-rd and 4-th sample standardized moments) are defined by
-
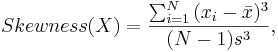 where
where 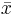 and s are the sample mean and sample standard deviation, respectively.
and s are the sample mean and sample standard deviation, respectively.
-
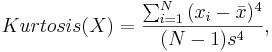 where
where 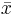 and s are the sample mean and sample standard deviation, respectively.
and s are the sample mean and sample standard deviation, respectively.
Examples
A Game of Chance
- Suppose we are offered to play a game of chance under these conditions: it costs us to play $1.50 and the awarded prices are {$1, $2, $3}. Assume the probabilities of winning each price are {0.6, 0.3, 0.1}, respectively. Should we play the game? What are our chances of winning/loosing? Let's let X=awarded price. Then X={1, 2, 3}.
| x | 1 | 2 | 3 |
| P(X=x) | 0.6 | 0.3 | 0.1 |
| x*P(X=x) | 0.6 | 0.6 | 0.3 |
Then the mean of this game (i.e., expected return or expectation) is computed as the weighted (by the outcome probabilities) average of all the outcome prices: ![E[X] = x_1P(X=x_1) + x_2P(X=x_2)+x_3P(X=x_3) = 1\times 0.6 + 2\times 0.3 + 3\times 0.1 = 1.5](/socr/uploads/math/0/b/c/0bcfa9cb8cff091987dd0d382c724b8e.png) . In other words, the expected return of this came is $1.5, which equals the entry fee, and hence the game is fair - neither the player nor the house has an advantage in this game (on the long run!) Of course, each streak of n games will produce different outcomes and may give small advantage to one side, however, on the long run, no one will make money.
. In other words, the expected return of this came is $1.5, which equals the entry fee, and hence the game is fair - neither the player nor the house has an advantage in this game (on the long run!) Of course, each streak of n games will produce different outcomes and may give small advantage to one side, however, on the long run, no one will make money.
The variance for this game is computed by VAR[X] = (x1 − 1.5)2P(X = x1) + (x2 − 1.5)2P(X = x2) + (x3 − 1.5)2P(X = x3) =
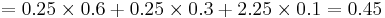 . Thus, the standard deviation is
. Thus, the standard deviation is ![SD[X] = \sqrt{VAR[X]}=0.67](/socr/uploads/math/2/b/c/2bc8ebb78cb6a8a87695ec1a37106d60.png) .
.
- Suppose now we alter the rules for the game of chance and the new pay-off is as follows:
| x | 0 | 1.5 | 3 |
| P(X=x) | 0.6 | 0.3 | 0.1 |
| x*P(X=x) | 0 | 0.45 | 0.3 |
- What is the new expected return of the game? Remember, the old expectation was equal to the entrance fee of $1.50, and the game was fair!
- The change in the pay-off of the game may be represented by this linear transformation
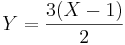 . Therefore, by our rules for computing expectations of linear functions,
. Therefore, by our rules for computing expectations of linear functions, 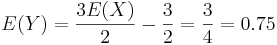 , and the game became clearly biased. Note how easy it is to compute E[Y], using this formula. At the same time, we could have computed the expectation of Y using first-principles (adding the values of the last row in the revised table above)!
, and the game became clearly biased. Note how easy it is to compute E[Y], using this formula. At the same time, we could have computed the expectation of Y using first-principles (adding the values of the last row in the revised table above)!
- You can play similar games under different conditions for the probability distribution of the prices using the SOCR Binomial Coin or Die experiments.
Children Gender Expectation Example
Suppose we conduct an (unethical!) experiment involving young couple planning to have children. Suppose, the couples are interested in the number of girls they will have, and each couple agrees to have children until one of the following 2 stopping criteria is met: (1) the couple has at least one child of each gender, or (2) the couple has at most 3 children! Let's denote the RV X ={number of Girls}. The distribution of X is given by:
| Observable Outcomes | {BBB} | {BG; GB; BBG} | {GGB} | {GGG} |
| x | 0 | 1 | 2 | 3 |
| P(X=x) | 1/8 | 5/8 | 1/8 | 1/8 |
| x*P(X=x) | 0 | 5/8 | 2/8 | 3/8 |
Therefore, the expected number of girls that each couple participating in this ("odd") experiment will have is given by E[X] = 0 + 5 / 8 + 2 / 8 + 3 / 8 = 1.25. What is the interpretation of this expectation?
Can you calculate the variance and standard deviation for this random variable?
Problems
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
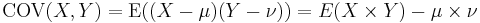
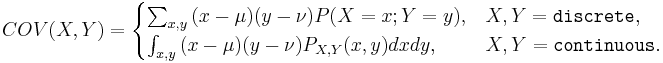
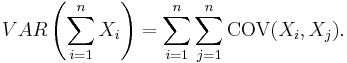
![E_s[X^k]={\sum_x{(x-\mu)^kP(X=x)} \over {(\sum_{x} (x-\mu)^2P(X=x))^{k/2}}}.](/socr/uploads/math/3/d/6/3d62db48d2060b237b49a1ea59dc43a1.png)
