AP Statistics Curriculum 2007 Distrib RV
From Socr
(→How do we use RVs?) |
|||
| (44 intermediate revisions not shown) | |||
| Line 2: | Line 2: | ||
=== Random Variables=== | === Random Variables=== | ||
| - | A '''random variable''' is a function or a mapping from a sample space into the real numbers (most of the time). In other words, a random variable assigns real values to outcomes of experiments. This mapping is called ''random'', as the output values of the mapping depend on the outcome of the experiment, which are indeed random. So, instead of studying the raw outcomes of experiments (e.g., define and compute probabilities), most of the time we study (or compute probabilities) | + | A '''random variable''' is a function or a mapping from a sample space into the real numbers (most of the time). In other words, a random variable assigns real values to outcomes of experiments. This mapping is called ''random'', as the output values of the mapping depend on the outcome of the experiment, which are indeed random. So, instead of studying the raw outcomes of experiments (e.g., define and compute probabilities), most of the time we study (or compute probabilities) the corresponding random variables instead. The [http://en.wikipedia.org/wiki/Random_variable formal general definition of random variables may be found here]. |
| - | ===Examples of | + | ===Examples of Random Variables=== |
| - | * '''Die''': In rolling a regular hexagonal die, the sample space is clearly and numerically well-defined | + | * '''Die''': In rolling a regular hexagonal die, the sample space is clearly and numerically well-defined. In this case, the random variable is the identity function assigning to each face of the die where the numerical value it represents. This the possible outcomes of the RV of this experiment are { 1, 2, 3, 4, 5, 6 }. You can see this explicit RV mapping in the [[SOCR_EduMaterials_Activities_DiceExperiment | SOCR Die Experiment]]. |
* '''Coin''': For a coin toss, a suitable space of possible outcomes is S={H, T} (for heads and tails). In this case these are not numerical values, so we can define a RV that maps these to numbers. For instance, we can define the RV <math>X: S \longrightarrow [0, 1]</math> as: <math>X(s) = \begin{cases}0,& s = \texttt{H},\\ | * '''Coin''': For a coin toss, a suitable space of possible outcomes is S={H, T} (for heads and tails). In this case these are not numerical values, so we can define a RV that maps these to numbers. For instance, we can define the RV <math>X: S \longrightarrow [0, 1]</math> as: <math>X(s) = \begin{cases}0,& s = \texttt{H},\\ | ||
1,& s = \texttt{T}.\end{cases}</math>. You can see this explicit RV mapping of heads and tails to numbers in the [[SOCR_EduMaterials_Activities_BinomialCoinExperiment | SOCR Coin Experiment]]. | 1,& s = \texttt{T}.\end{cases}</math>. You can see this explicit RV mapping of heads and tails to numbers in the [[SOCR_EduMaterials_Activities_BinomialCoinExperiment | SOCR Coin Experiment]]. | ||
| - | * '''Card''': Suppose we draw a [[ | 5-card hand from a standard 52-card deck]] and we are interested in the probability that the hand contains at least one pair of cards with identical denomination. | + | * '''Card''': Suppose we draw a [[SOCR_EduMaterials_Activities_CardExperiment | 5-card hand from a standard 52-card deck]] and we are interested in the probability that the hand contains at least one pair of cards with identical denomination. Since the sample space of this experiment is large, it should be difficult to list all possible outcomes. However, we can assign a random variable <math>X(s) = \begin{cases}0,& s = \texttt{no-pair},\\ |
1,& s = \texttt{at-least-1-pair}.\end{cases}</math> and try to compute the probability of P(X=1), the chance that the hand contains a pair. You can see this explicit RV mapping and the calculations of this probability at the [[SOCR_EduMaterials_Activities_CardExperiment | SOCR Card Experiment]]. | 1,& s = \texttt{at-least-1-pair}.\end{cases}</math> and try to compute the probability of P(X=1), the chance that the hand contains a pair. You can see this explicit RV mapping and the calculations of this probability at the [[SOCR_EduMaterials_Activities_CardExperiment | SOCR Card Experiment]]. | ||
| + | * '''A Pair of Dice''': Suppose we roll a pair of dice and the random variable X represents their sum. Of course we could have chosen any function of the outcomes of the 2 dice, but the most common game-like situation is to look at the total sum as an outcome. The figure below explicitly defines the sample space and the RV mapping from he sample space (S) into the real numbers (R). | ||
| + | <center>[[Image:SOCR_EBook_Distrib_RV_Fig3.png|500px]]</center> | ||
| - | === | + | ===Probability density/mass and (cumulative) distribution functions=== |
| - | + | * The '''probability density''' or '''probability mass''' function, for a continuous or discrete random variable, is the function defined by the probability of the subset of the sample space, <math>\{s \in S \} \subset S</math>, which is mapped by the random variable ''X'' to the real value ''x'' (i.e., ''X(s)=x''): | |
| + | : <math>p(x) = P(\{s \in S \} | X(s) = x)</math>, for each ''x''. | ||
| - | * ''' | + | * The '''cumulative distribution function''' (cdf) F(x) of any random variable ''X'' with probability mass or density function ''p(x)'' is defined as the total probability of all <math>\{s \in S \} \subset S</math>, where <math>X(s)\leq x</math>: |
| + | : <math>F(x)=P(X\leq x)= \begin{cases}{ \sum_{y: y\leq x} {p(y)}},& X = \texttt{Discrete-RV},\\ | ||
| + | {\int_{-\infty}^{x} {p(y)dy}},& X = \texttt{continuous-RV}.\end{cases}</math>, for all x. | ||
| + | |||
| + | ====PDF Example==== | ||
| + | The [http://en.wikipedia.org/wiki/Benford's_law Benford's Law] states that the ''probability'' of the first digit (''d'') in a large number of integer observations (<math>d\not=0</math>) is given by | ||
| + | <center> <math>P(d) = \log(d+1) - log(d) = \log{d+1 \over d}</math>, for <math>d = 1,2,\cdots,9.</math></center> | ||
| + | |||
| + | Note that this probability definition determines a discrete probability (mass) distribution: | ||
| + | |||
| + | <center><math>\sum_{d=1}^9{P(d)}=\log{2\over 1}+\log{3\over 2}+\log{4\over 3}+ \cdots +\log{10\over 9}=</math> | ||
| + | <math>\log({{2\over 1} {3\over 2} {4\over 3} \cdots{10\over 9}}) = \log{10\over 1} = 1</math> </center> | ||
| - | * '''Cumulative | + | <center> |
| + | {| class="wikitable" style="text-align:center; width:75%" border="1" | ||
| + | |- | ||
| + | | ''d'' || 1 || 2 || 3 || 4 || 5 || 6 || 7 || 8 || 9 | ||
| + | |- | ||
| + | | <math>P(d)</math> || 0.301 || 0.176 || 0.125 || 0.097 || 0.079 || 0.067 || 0.058 || 0.051 || 0.046 | ||
| + | |} | ||
| + | </center> | ||
| + | |||
| + | The explanation of the [http://en.wikipedia.org/wiki/Benford's_law Benford's Law] may be summarized as follows: The distribution of the first digits must be independent of the measuring units used in observing/recording the integer measurements. For instance, this means that if we had observed length/distance in ''inches'' or ''centimeters'' (inches and centimeters are linearly dependent, <math>1in = 2.54cm</math>), the distribution of the first digit of the measurement must be identical. So, there are about three centimeters for each inch. Thus, the probability that the first digit of a length observation is ''1in'' must be the same as the probability that the first digit of a length in ''centimeters'' starts with either 2 or 3 (with standard round off). Similarly, for observations of ''2in'', they need to have their centimeter counterparts either ''5cm'' or ''6cm''. Observations of ''3in'' will correspond to 7 or 8 centimeters, etc. In other words, this distribution must be [http://en.wikipedia.org/wiki/Scale_invariant scale invariant]. | ||
| + | |||
| + | |||
| + | The only distribution that obeys this property is the one whose logarithm is uniformly distributed. In this case, the logarithms of the numbers are uniformly distributed -- <math>P(100\leq x \leq 1,000)</math> = <math>P(2\leq \log(x)\leq 3)</math> is the same as the probability <math>P(10,000\leq x \leq 100,000)</math> = <math>P(4\leq \log(x)\leq 5)</math>. Examples of such exponentially growing numerical measurements are incomes, stock prices and computational power. | ||
| + | |||
| + | ===How to Use RVs?=== | ||
| + | There are 3 important quantities that we are always interested in when we study random processes. Each of these may be phrased in terms of RVs, which simplifies their calculations. | ||
| + | |||
| + | * '''Probability Density Function''' (PDF): What is the probability of <math>P(X=x_o)</math>? For instance, in the card example above, we may be interested in [[SOCR_EduMaterials_Activities_CardExperiment#Applications | P(exactly 1 pair) = P(X=1) = P(1 pair only) = 0.422569]]. Or in the die example, we may want to know P(Even number turns up) = <math>P(X \in \{2, 4, 6 \}) = 0.5</math>. | ||
| + | |||
| + | * '''Cumulative Distribution Function''' (CDF): <math>P(X <x_o)</math>, for all <math>x_o</math>. For instance, in the (fair) die example we have the following discrete density (mass) and cumulative distribution table: | ||
<center> | <center> | ||
{| class="wikitable" style="text-align:center; width:75%" border="1" | {| class="wikitable" style="text-align:center; width:75%" border="1" | ||
| Line 26: | Line 59: | ||
| x || 1 || 2 || 3 || 4 || 5 || 6 | | x || 1 || 2 || 3 || 4 || 5 || 6 | ||
|- | |- | ||
| - | | P(X | + | | PDF<math>P(X = x)</math> || 1/6 || 1/6 || 1/6 || 1/6 || 1/6 || 1/6 |
| + | |- | ||
| + | | CDF <math>P(X\leq x)</math> || 1/6 || 2/6 || 3/6 || 4/6 || 5/6 || 1 | ||
|} | |} | ||
</center> | </center> | ||
| - | * | + | * [[AP_Statistics_Curriculum_2007_Distrib_MeanVar | Mean/Expected Value]]: Most natural processes may be characterized, via probability distribution of an appropriate RV, in terms of a small number of parameters. These parameters simplify the practical interpretation of the process or phenomena we study. For example, it is often enough to know what the process (or RV) ''average value'' is. This is the concept of '''expected value''' (or '''mean''') of a random variable, denoted E[X]. The expected value is the point of gravitational balance of the distribution of the RV. |
Obviously, we may define a large number of RV for the same process. When are [http://en.wikipedia.org/wiki/Random_variable#Equivalence_of_random_variables two RVs equivalent is dependent on the definition of equivalence]? | Obviously, we may define a large number of RV for the same process. When are [http://en.wikipedia.org/wiki/Random_variable#Equivalence_of_random_variables two RVs equivalent is dependent on the definition of equivalence]? | ||
| + | |||
| + | ===Comparing Data and Model Distributions=== | ||
| + | To illustrate one example of using distributions for solving practical problems, we consider the [[SOCR_Data_Dinov_020108_HeightsWeights | large human weight and height dataset]]. You can use all 25,000 records or just the first 200 of these measurements to follow the protocol below: | ||
| + | * Copy the [[SOCR_Data_Dinov_020108_HeightsWeights| weight and height data]] into the [http://socr.ucla.edu/htmls/SOCR_Charts.html data tab of any of the SOCR Charts] (first clear the default data, then select column 1 heading, and click the '''Paste''' button). This allows you to manipulate each of the 3 data columns independently. | ||
| + | * Select (highlight with the mouse) one of the columns (e.g., weights or heights) in the SOCR Chart and click the '''Copy''' button. This stores only the data in the chosen column in your mouse buffer. | ||
| + | * Go to the [http://socr.ucla.edu/htmls/SOCR_Modeler.html SOCR Modeler] and paste the data in the first column in the '''Data''' tab using the '''Paste''' button. | ||
| + | * Select the ''NormalFit_Modeler'' from the drop-down list on the top-left corner. This is the first model you will be fitting to your data. | ||
| + | * Select the 3 check-boxes (''Estimate Parameters'', ''Scale Up'', and ''Raw Data''). | ||
| + | * Go to the '''Graphs''' tab and adjust the 3 sliders on the top to get a clear view of your data distribution (sample histogram) and the model distribution function (solid red curve). | ||
| + | * The '''Results''' tab will contain the (data-driven) estimates of the parameters for this specific distribution model (in this case [[EBook#Chapter_V:_Normal_Probability_Distribution |Normal]]). | ||
| + | * You can plug these parameters (mean and standard deviation) into the [http://socr.ucla.edu/htmls/dist/Normal_Distribution.html SOCR Normal Distribution Applet] and make inference about your population based on this [[EBook#Chapter_V:_Normal_Probability_Distribution |Normal distribution]] model. | ||
| + | * Validate that the probabilities of various interesting events (e.g., 68<=Height<70) computed via either using the sample histogram of the data or via the model distribution are very similar. | ||
| + | * Try fitting another distribution model to your data using the [http://socr.ucla.edu/htmls/SOCR_Modeler.html SOCR Modeler]. For example, choose the mixture-of-Normals model ('''MixedFit_Modeler''') and repeat this process. Can you identify possible gender effects in either height or weight of the subjects in your sample? If so, what are the Male and Female distribution models? Can these be used to predict the gender of subjects (based on their weight or height)? | ||
| + | * Note that the '''Results''' tab also shows some statistics quantifying how good your chosen distribution model is to approximate the (sample) data histogram. | ||
| + | |||
| + | ===The Web of Distributions=== | ||
| + | There is a large number of families of distributions and distribution classification schemes. | ||
| + | |||
| + | : The most common way to describe the universe of distributions is to partition them into categories. For example, [http://en.wikipedia.org/wiki/Category:Continuous_distributions Continuous Distributions] and [http://en.wikipedia.org/wiki/Category:Discrete_distributions Discrete Distributions]; [http://en.wikipedia.org/wiki/Marginal_distribution marginal] and [http://en.wikipedia.org/wiki/Joint_distribution joint] distributions; [http://en.wikipedia.org/wiki/Probability_distribution#With_finite_support finitely] and [http://en.wikipedia.org/wiki/Probability_distribution#With_infinite_support infinitely] supported, etc. | ||
| + | |||
| + | |||
| + | : [http://distributome.org/ SOCR Distributome Project] and the [[SOCR_EduMaterials_DistributionsActivities | SOCR Distribution activities]] illustrate how to use technology to compute probabilities for events arising from many different processes. | ||
| + | |||
| + | |||
| + | : The image below shows some of the relations between [[About_pages_for_SOCR_Distributions|commonly used distributions]]. Many of these [[EBook#Chapter_VI:_Relations_Between_Distributions |relations will be explored later]]. | ||
| + | |||
| + | <center>[[Image:SOCR_EBook_Dinov_DistributionRelations_031108_Fig1.jpg|500px]]</center> | ||
| + | |||
| + | : [http://distributome.org/ The SOCR Distributome applet provides an interactive graphical interface for exploring the relations between different distributions]. | ||
| + | |||
| + | ===Generating Probability Tables=== | ||
| + | Once can use R (and many other programming languages) to generate probability tables like the [http://socr.umich.edu/Applets/index.html#Tables popular SOCR Probability Tables]. You can also use the [http://socr.ucla.edu/htmls/dist/ Java Applets] or the [http://www.distributome.org/V3/calc/ HTML5/JavaScript Webapps] for interactive | ||
| + | F-Distribution calculations and obtain more dense and accurate measures of probability or critical values. | ||
| + | |||
| + | The following example generates one of the [http://socr.umich.edu/Applets/F_Table.html F distribution tables: $F(\alpha=0.001, df.num, df.deno)$]: | ||
| + | |||
| + | # Define the right-tail probability of interest $\alpha=0.001$ | ||
| + | right_tail_p <- 0.001 | ||
| + | |||
| + | # Define the vectors storing the indices corresponding to numerator (n1) and denominator (n2, row) | ||
| + | # degrees of freedom for $F(\alpha, n_1, n_2)$. Note that Inf corresponds to $\infty$. | ||
| + | |||
| + | n1 <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 15, 20, 24, 30, 40, 60, 120, Inf) | ||
| + | n2 <- c(1:30, 40, 60, 120, Inf) | ||
| + | |||
| + | # Define precision (4-decimal point accuracy) | ||
| + | options(digits=4) | ||
| + | |||
| + | # Generate an empty matrix of critical f-values | ||
| + | f_table <- matrix(ncol=length(n1), nrow=length(n2)) | ||
| + | |||
| + | # Use the The F Distribution quantile function to fill in the matrix values in a nested 2-loop | ||
| + | # Recall that the density (df), distribution function (pf), quantile function (qf) and random generation (rf) for the F distribution | ||
| + | |||
| + | for (i in 1:length(n2)){ | ||
| + | for (j in 1:length(n1)){ | ||
| + | f_table[i,j] <- qf(right_tail_p, n1[j], n2[i], lower.tail = FALSE) | ||
| + | } | ||
| + | } | ||
| + | |||
| + | # Print results | ||
| + | f_table | ||
| + | |||
| + | # label rows and columns | ||
| + | rownames(f_table) <- n2; colnames(f_table) <- n1 | ||
| + | |||
| + | # save results to a file | ||
| + | write.table(f_table, file="C:\\User\\f_table.txt") | ||
| + | |||
| + | ===[[EBook_Problems_Distrib_RV|Problems]]=== | ||
<hr> | <hr> | ||
Current revision as of 18:38, 18 March 2016
Contents |
General Advance-Placement (AP) Statistics Curriculum - Random Variables and Probability Distributions
Random Variables
A random variable is a function or a mapping from a sample space into the real numbers (most of the time). In other words, a random variable assigns real values to outcomes of experiments. This mapping is called random, as the output values of the mapping depend on the outcome of the experiment, which are indeed random. So, instead of studying the raw outcomes of experiments (e.g., define and compute probabilities), most of the time we study (or compute probabilities) the corresponding random variables instead. The formal general definition of random variables may be found here.
Examples of Random Variables
- Die: In rolling a regular hexagonal die, the sample space is clearly and numerically well-defined. In this case, the random variable is the identity function assigning to each face of the die where the numerical value it represents. This the possible outcomes of the RV of this experiment are { 1, 2, 3, 4, 5, 6 }. You can see this explicit RV mapping in the SOCR Die Experiment.
- Coin: For a coin toss, a suitable space of possible outcomes is S={H, T} (for heads and tails). In this case these are not numerical values, so we can define a RV that maps these to numbers. For instance, we can define the RV
![X: S \longrightarrow [0, 1]](/socr/uploads/math/9/5/e/95e11d7a452f746b687a6e814bc71747.png) as:
as: 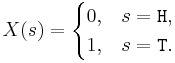 . You can see this explicit RV mapping of heads and tails to numbers in the SOCR Coin Experiment.
. You can see this explicit RV mapping of heads and tails to numbers in the SOCR Coin Experiment.
- Card: Suppose we draw a 5-card hand from a standard 52-card deck and we are interested in the probability that the hand contains at least one pair of cards with identical denomination. Since the sample space of this experiment is large, it should be difficult to list all possible outcomes. However, we can assign a random variable
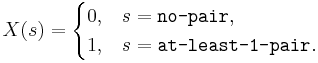 and try to compute the probability of P(X=1), the chance that the hand contains a pair. You can see this explicit RV mapping and the calculations of this probability at the SOCR Card Experiment.
and try to compute the probability of P(X=1), the chance that the hand contains a pair. You can see this explicit RV mapping and the calculations of this probability at the SOCR Card Experiment.
- A Pair of Dice: Suppose we roll a pair of dice and the random variable X represents their sum. Of course we could have chosen any function of the outcomes of the 2 dice, but the most common game-like situation is to look at the total sum as an outcome. The figure below explicitly defines the sample space and the RV mapping from he sample space (S) into the real numbers (R).
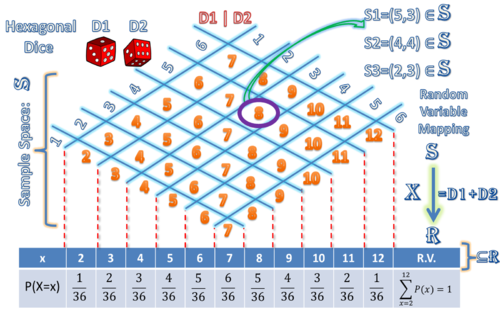
Probability density/mass and (cumulative) distribution functions
- The probability density or probability mass function, for a continuous or discrete random variable, is the function defined by the probability of the subset of the sample space,
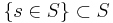 , which is mapped by the random variable X to the real value x (i.e., X(s)=x):
, which is mapped by the random variable X to the real value x (i.e., X(s)=x):
-
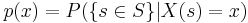 , for each x.
, for each x.
- The cumulative distribution function (cdf) F(x) of any random variable X with probability mass or density function p(x) is defined as the total probability of all
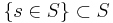 , where
, where 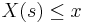 :
:
-
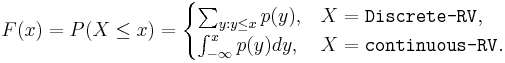 , for all x.
, for all x.
PDF Example
The Benford's Law states that the probability of the first digit (d) in a large number of integer observations (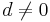 ) is given by
) is given by
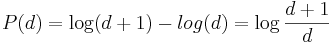 , for
, for 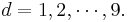
Note that this probability definition determines a discrete probability (mass) distribution:
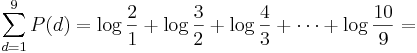
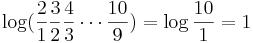
| d | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| P(d) | 0.301 | 0.176 | 0.125 | 0.097 | 0.079 | 0.067 | 0.058 | 0.051 | 0.046 |
The explanation of the Benford's Law may be summarized as follows: The distribution of the first digits must be independent of the measuring units used in observing/recording the integer measurements. For instance, this means that if we had observed length/distance in inches or centimeters (inches and centimeters are linearly dependent, 1in = 2.54cm), the distribution of the first digit of the measurement must be identical. So, there are about three centimeters for each inch. Thus, the probability that the first digit of a length observation is 1in must be the same as the probability that the first digit of a length in centimeters starts with either 2 or 3 (with standard round off). Similarly, for observations of 2in, they need to have their centimeter counterparts either 5cm or 6cm. Observations of 3in will correspond to 7 or 8 centimeters, etc. In other words, this distribution must be scale invariant.
The only distribution that obeys this property is the one whose logarithm is uniformly distributed. In this case, the logarithms of the numbers are uniformly distributed -- 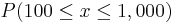 =
= 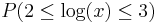 is the same as the probability
is the same as the probability 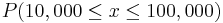 =
= 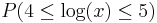 . Examples of such exponentially growing numerical measurements are incomes, stock prices and computational power.
. Examples of such exponentially growing numerical measurements are incomes, stock prices and computational power.
How to Use RVs?
There are 3 important quantities that we are always interested in when we study random processes. Each of these may be phrased in terms of RVs, which simplifies their calculations.
- Probability Density Function (PDF): What is the probability of P(X = xo)? For instance, in the card example above, we may be interested in P(exactly 1 pair) = P(X=1) = P(1 pair only) = 0.422569. Or in the die example, we may want to know P(Even number turns up) =
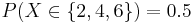 .
.
- Cumulative Distribution Function (CDF): P(X < xo), for all xo. For instance, in the (fair) die example we have the following discrete density (mass) and cumulative distribution table:
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| PDFP(X = x) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
CDF 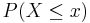 | 1/6 | 2/6 | 3/6 | 4/6 | 5/6 | 1 |
- Mean/Expected Value: Most natural processes may be characterized, via probability distribution of an appropriate RV, in terms of a small number of parameters. These parameters simplify the practical interpretation of the process or phenomena we study. For example, it is often enough to know what the process (or RV) average value is. This is the concept of expected value (or mean) of a random variable, denoted E[X]. The expected value is the point of gravitational balance of the distribution of the RV.
Obviously, we may define a large number of RV for the same process. When are two RVs equivalent is dependent on the definition of equivalence?
Comparing Data and Model Distributions
To illustrate one example of using distributions for solving practical problems, we consider the large human weight and height dataset. You can use all 25,000 records or just the first 200 of these measurements to follow the protocol below:
- Copy the weight and height data into the data tab of any of the SOCR Charts (first clear the default data, then select column 1 heading, and click the Paste button). This allows you to manipulate each of the 3 data columns independently.
- Select (highlight with the mouse) one of the columns (e.g., weights or heights) in the SOCR Chart and click the Copy button. This stores only the data in the chosen column in your mouse buffer.
- Go to the SOCR Modeler and paste the data in the first column in the Data tab using the Paste button.
- Select the NormalFit_Modeler from the drop-down list on the top-left corner. This is the first model you will be fitting to your data.
- Select the 3 check-boxes (Estimate Parameters, Scale Up, and Raw Data).
- Go to the Graphs tab and adjust the 3 sliders on the top to get a clear view of your data distribution (sample histogram) and the model distribution function (solid red curve).
- The Results tab will contain the (data-driven) estimates of the parameters for this specific distribution model (in this case Normal).
- You can plug these parameters (mean and standard deviation) into the SOCR Normal Distribution Applet and make inference about your population based on this Normal distribution model.
- Validate that the probabilities of various interesting events (e.g., 68<=Height<70) computed via either using the sample histogram of the data or via the model distribution are very similar.
- Try fitting another distribution model to your data using the SOCR Modeler. For example, choose the mixture-of-Normals model (MixedFit_Modeler) and repeat this process. Can you identify possible gender effects in either height or weight of the subjects in your sample? If so, what are the Male and Female distribution models? Can these be used to predict the gender of subjects (based on their weight or height)?
- Note that the Results tab also shows some statistics quantifying how good your chosen distribution model is to approximate the (sample) data histogram.
The Web of Distributions
There is a large number of families of distributions and distribution classification schemes.
- The most common way to describe the universe of distributions is to partition them into categories. For example, Continuous Distributions and Discrete Distributions; marginal and joint distributions; finitely and infinitely supported, etc.
- SOCR Distributome Project and the SOCR Distribution activities illustrate how to use technology to compute probabilities for events arising from many different processes.
- The image below shows some of the relations between commonly used distributions. Many of these relations will be explored later.

Generating Probability Tables
Once can use R (and many other programming languages) to generate probability tables like the popular SOCR Probability Tables. You can also use the Java Applets or the HTML5/JavaScript Webapps for interactive F-Distribution calculations and obtain more dense and accurate measures of probability or critical values.
The following example generates one of the F distribution tables: $F(\alpha=0.001, df.num, df.deno)$:
# Define the right-tail probability of interest $\alpha=0.001$
right_tail_p <- 0.001
# Define the vectors storing the indices corresponding to numerator (n1) and denominator (n2, row)
# degrees of freedom for $F(\alpha, n_1, n_2)$. Note that Inf corresponds to $\infty$.
n1 <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 15, 20, 24, 30, 40, 60, 120, Inf)
n2 <- c(1:30, 40, 60, 120, Inf)
# Define precision (4-decimal point accuracy)
options(digits=4)
# Generate an empty matrix of critical f-values
f_table <- matrix(ncol=length(n1), nrow=length(n2))
# Use the The F Distribution quantile function to fill in the matrix values in a nested 2-loop
# Recall that the density (df), distribution function (pf), quantile function (qf) and random generation (rf) for the F distribution
for (i in 1:length(n2)){
for (j in 1:length(n1)){
f_table[i,j] <- qf(right_tail_p, n1[j], n2[i], lower.tail = FALSE)
}
}
# Print results
f_table
# label rows and columns
rownames(f_table) <- n2; colnames(f_table) <- n1
# save results to a file
write.table(f_table, file="C:\\User\\f_table.txt")
Problems
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
