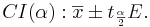AP Statistics Curriculum 2007 Estim S Mean
From Socr
| Line 4: | Line 4: | ||
=== Point Estimation of a Population Mean=== | === Point Estimation of a Population Mean=== | ||
| - | + | The population mean may also be estimated by the sample average using a small sample. That is the sample average <math>\overline{X_n}={1\over n}\sum_{i=1}^n{X_i}</math>, constructed from a random sample of the procees {<math>X_1, X_2, X_3, \cdots , X_n</math>}, is an [http://en.wikipedia.org/wiki/Estimator_bias unbiased] estimate of the population mean <math>\mu</math>, if it exists! Note that the [[AP_Statistics_Curriculum_2007_EDA_Center | sample average may be susceptible to outliers]]. | |
===Interval Estimation of a Population Mean=== | ===Interval Estimation of a Population Mean=== | ||
| - | For | + | For small samples, interval estimation of the population means (or '''Confidence intervals''') are constructed as follows. Choose a confidence level <math>(1-\alpha)100%</math>, where <math>\alpha</math> is small (e.g., 0.1, 0.05, 0.025, 0.01, 0.001, etc.). Then a <math>(1-\alpha)100%</math> confidence interval for <math>\mu</math> is defined in terms of the T-distribution: |
| - | : <math>CI(\alpha): \overline{x} \pm | + | : <math>CI(\alpha): \overline{x} \pm t_{\alpha\over 2} E.</math> |
* The '''margin of error''' E is defined as | * The '''margin of error''' E is defined as | ||
| Line 17: | Line 17: | ||
<math>SE(\overline {x}) = {1\over \sqrt{n}} \sqrt{\sum_{i=1}^n{(x_i-\overline{x})^2\over n-1}}</math> | <math>SE(\overline {x}) = {1\over \sqrt{n}} \sqrt{\sum_{i=1}^n{(x_i-\overline{x})^2\over n-1}}</math> | ||
| - | * <math> | + | * <math>t_{\alpha\over 2}</math> is the critical value for the T(df=sample-size -1) distribution distribution at <math>{\alpha\over 2}</math>. |
===Example=== | ===Example=== | ||
| - | + | To parallel the example in the [[AP_Statistics_Curriculum_2007#Estimating_a_Population_Mean:_Large_Samples |large sample case]], we consider again the ''number of sentences per advertisement'' as a measure of readability for magazine advertisements. A random sample of the number of sentences found in 10 magazine advertisements is listed. Use this sample to find ''point estimate'' for the population mean <math>\mu</math>. | |
<center> | <center> | ||
{| class="wikitable" style="text-align:center; width:75%" border="1" | {| class="wikitable" style="text-align:center; width:75%" border="1" | ||
|- | |- | ||
| - | | 16 || 9 || 14 || 11|| 17 || 12|| 99 || 18 || 13|| | + | | 16 || 9 || 14 || 11|| 17 || 12|| 99 || 18 || 13|| 12 |
|} | |} | ||
</center> | </center> | ||
| - | A ''confidence interval estimate'' of <math>\mu</math> is a range of values used to estimate a population parameter (interval estimates are normally used more than point estimates because it is very unlikely that the sample mean would match exactly with the population mean) The interval estimate uses a margin of error about the point estimate. | + | A ''confidence interval estimate'' of <math>\mu</math> is a range of values used to estimate a population parameter (interval estimates are normally used more than point estimates because it is very unlikely that the sample mean would match exactly with the population mean) The interval estimate uses a margin of error about the point estimate. |
Before you find an interval estimate, you should first determine how confident you want to be that your interval estimate contains the population mean. | Before you find an interval estimate, you should first determine how confident you want to be that your interval estimate contains the population mean. | ||
* [[AP_Statistics_Curriculum_2007_Normal_Critical | Recall these critical values for Standard Normal distribution]]: | * [[AP_Statistics_Curriculum_2007_Normal_Critical | Recall these critical values for Standard Normal distribution]]: | ||
| - | :80% confidence (0.80), <math>\alpha=0.1</math>, | + | :80% confidence (0.80), <math>\alpha=0.1</math>, [http://socr.ucla.edu/Applets.dir/T-table.html t<sub>df=9</sub> = 1.383] |
| - | :90% confidence (0.90), <math>\alpha=0.05</math>, | + | :90% confidence (0.90), <math>\alpha=0.05</math>, [http://socr.ucla.edu/Applets.dir/T-table.html t<sub>df=9</sub> = 1.833] |
| - | :95% confidence (0.95), <math>\alpha=0.025</math>, | + | :95% confidence (0.95), <math>\alpha=0.025</math>, [http://socr.ucla.edu/Applets.dir/T-table.html t<sub>df=9</sub> = 2.262] |
| - | :99% confidence (0.99), <math>\alpha=0.005</math>, | + | :99% confidence (0.99), <math>\alpha=0.005</math>, [http://socr.ucla.edu/Applets.dir/T-table.html t<sub>df=9</sub> = 3.250] |
| + | |||
| + | Notice that for a fixed <math>\alpha</math>, the ''t-critical values'' (for any degree-of-freedom) exceeds the [[AP_Statistics_Curriculum_2007#Estimating_a_Population_Mean:_Large_Samples |corresponding normal z-critical values]], which are used int he large-sample interval estimation. | ||
====Known Variance==== | ====Known Variance==== | ||
Suppose that we know the variance for the ''number of sentences per advertisement'' example above is known to be 256 (so the population standard deviation is <math>\sigma=16</math>). | Suppose that we know the variance for the ''number of sentences per advertisement'' example above is known to be 256 (so the population standard deviation is <math>\sigma=16</math>). | ||
| - | * For <math>\alpha=0.1</math>, the <math> | + | * For <math>\alpha=0.1</math>, the <math>80% CI(\mu)</math> is constructed by: |
| - | <center> <math>\overline{x}\pm 1. | + | <center> <math>\overline{x}\pm 1.383{16\over \sqrt{10}}=14.77 \pm 1.28{16\over \sqrt{30}}=[15.10 ; 29.10]</math></center> |
* For <math>\alpha=0.05</math>, the <math>90% CI(\mu)</math> is constructed by: | * For <math>\alpha=0.05</math>, the <math>90% CI(\mu)</math> is constructed by: | ||
| - | <center> <math>\overline{x}\pm 1. | + | <center> <math>\overline{x}\pm 1.833{16\over \sqrt{10}}=14.77 \pm 1.645{16\over \sqrt{30}}=[12.83 ; 31.37]</math></center> |
| - | * For <math>\alpha=0.005</math>, the <math> | + | * For <math>\alpha=0.005</math>, the <math>99% CI(\mu)</math> is constructed by: |
| - | <center> <math>\overline{x}\pm | + | <center> <math>\overline{x}\pm 3.250{16\over \sqrt{10}}=14.77 \pm 2.575{16\over \sqrt{30}}=[5.66 ; 38.54]</math></center> |
Notice the increase of the CI's (directly related to the decrease of <math>\alpha</math>) reflecting our choice for higher confidence. | Notice the increase of the CI's (directly related to the decrease of <math>\alpha</math>) reflecting our choice for higher confidence. | ||
====Unknown variance==== | ====Unknown variance==== | ||
| - | Suppose that we do '''not''' know the variance for the ''number of sentences per advertisement'' but use the sample variance | + | Suppose that we do '''not''' know the variance for the ''number of sentences per advertisement'' but use the sample variance 737.88 as an estimate (so the sample standard deviation is <math>s=\hat{\sigma}=27.16390579</math>). |
| - | * For <math>\alpha=0.1</math>, the <math> | + | * For <math>\alpha=0.1</math>, the <math>80% CI(\mu)</math> is constructed by: |
| - | <center> <math>\overline{x}\pm 1. | + | <center> <math>\overline{x}\pm 1.383{27.16390579\over \sqrt{10}}=14.77 \pm 1.28{16\over \sqrt{30}}=[10.22 ; 33.98]</math></center> |
* For <math>\alpha=0.05</math>, the <math>90% CI(\mu)</math> is constructed by: | * For <math>\alpha=0.05</math>, the <math>90% CI(\mu)</math> is constructed by: | ||
| - | <center> <math>\overline{x}\pm 1. | + | <center> <math>\overline{x}\pm 1.833{27.16390579\over \sqrt{10}}=14.77 \pm 1.645{16\over \sqrt{30}}=[6.35 ; 37.85]</math></center> |
| - | * For <math>\alpha=0.005</math>, the <math> | + | * For <math>\alpha=0.005</math>, the <math>99% CI(\mu)</math> is constructed by: |
| - | <center> <math>\overline{x}\pm | + | <center> <math>\overline{x}\pm 3.250{27.16390579 \over \sqrt{10}}=14.77 \pm 2.575{16\over \sqrt{30}}=[-5.82 ; 50.02]</math></center> |
Notice the increase of the CI's (directly related to the decrease of <math>\alpha</math>) reflecting our choice for higher confidence. | Notice the increase of the CI's (directly related to the decrease of <math>\alpha</math>) reflecting our choice for higher confidence. | ||
| Line 69: | Line 71: | ||
*See the [[SOCR_EduMaterials_Activities_CoinfidenceIntervalExperiment | SOCR Confidence Interval Experiment]]. | *See the [[SOCR_EduMaterials_Activities_CoinfidenceIntervalExperiment | SOCR Confidence Interval Experiment]]. | ||
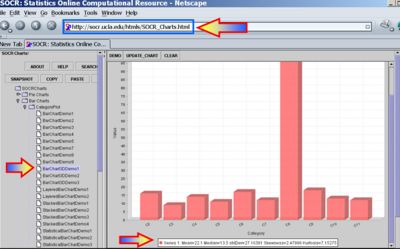
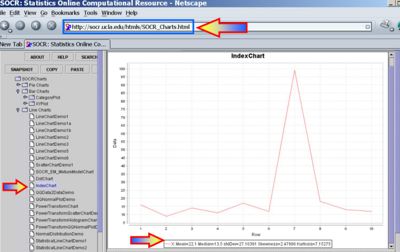
* Sample statistics, like the sample-mean and the sample-variance, may be easily obtained using [http://socr.ucla.edu/htmls/SOCR_Charts.html SOCR Charts]. The images below illustrate this functionality (based on the '''Bar-Chart''' and '''Index-Chart''') using the 30 observations of the number of sentences per advertisement, [[AP_Statistics_Curriculum_2007_Estim_L_Mean#Example | reported above]]. | * Sample statistics, like the sample-mean and the sample-variance, may be easily obtained using [http://socr.ucla.edu/htmls/SOCR_Charts.html SOCR Charts]. The images below illustrate this functionality (based on the '''Bar-Chart''' and '''Index-Chart''') using the 30 observations of the number of sentences per advertisement, [[AP_Statistics_Curriculum_2007_Estim_L_Mean#Example | reported above]]. | ||
| - | <center>[[Image: | + | <center>[[Image:SOCR_EBook_Dinov_Estimates_L_Mean_020208_Fig3.jpg|400px]] |
| - | [[Image: | + | [[Image:SOCR_EBook_Dinov_Estimates_L_Mean_020208_Fig4.jpg|400px]]</center> |
<hr> | <hr> | ||
Revision as of 19:55, 3 February 2008
Contents |
General Advance-Placement (AP) Statistics Curriculum - Estimating a Population Mean: Samll Samples
Now we discuss estimation when the sample-sizes are small, typically < 30 observations. Naturally, the point estimates are less precise and the interval estimates produce wider intervals, compared to the case of large-samples.
Point Estimation of a Population Mean
The population mean may also be estimated by the sample average using a small sample. That is the sample average 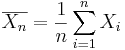 , constructed from a random sample of the procees {
, constructed from a random sample of the procees {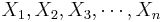 }, is an unbiased estimate of the population mean μ, if it exists! Note that the sample average may be susceptible to outliers.
}, is an unbiased estimate of the population mean μ, if it exists! Note that the sample average may be susceptible to outliers.
Interval Estimation of a Population Mean
For small samples, interval estimation of the population means (or Confidence intervals) are constructed as follows. Choose a confidence level (1 − α)100%, where α is small (e.g., 0.1, 0.05, 0.025, 0.01, 0.001, etc.). Then a (1 − α)100% confidence interval for μ is defined in terms of the T-distribution:
- The margin of error E is defined as

- The Standard Error of the estimate
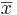 is obtained by replacing the unknown population standard deviation by the sample standard deviation:
is obtained by replacing the unknown population standard deviation by the sample standard deviation:
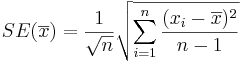
-
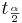 is the critical value for the T(df=sample-size -1) distribution distribution at
is the critical value for the T(df=sample-size -1) distribution distribution at 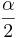 .
.
Example
To parallel the example in the large sample case, we consider again the number of sentences per advertisement as a measure of readability for magazine advertisements. A random sample of the number of sentences found in 10 magazine advertisements is listed. Use this sample to find point estimate for the population mean μ.
| 16 | 9 | 14 | 11 | 17 | 12 | 99 | 18 | 13 | 12 |
A confidence interval estimate of μ is a range of values used to estimate a population parameter (interval estimates are normally used more than point estimates because it is very unlikely that the sample mean would match exactly with the population mean) The interval estimate uses a margin of error about the point estimate.
Before you find an interval estimate, you should first determine how confident you want to be that your interval estimate contains the population mean.
- 80% confidence (0.80), α = 0.1, tdf=9 = 1.383
- 90% confidence (0.90), α = 0.05, tdf=9 = 1.833
- 95% confidence (0.95), α = 0.025, tdf=9 = 2.262
- 99% confidence (0.99), α = 0.005, tdf=9 = 3.250
Notice that for a fixed α, the t-critical values (for any degree-of-freedom) exceeds the corresponding normal z-critical values, which are used int he large-sample interval estimation.
Known Variance
Suppose that we know the variance for the number of sentences per advertisement example above is known to be 256 (so the population standard deviation is σ = 16).
- For α = 0.1, the 80%CI(μ) is constructed by:
![\overline{x}\pm 1.383{16\over \sqrt{10}}=14.77 \pm 1.28{16\over \sqrt{30}}=[15.10 ; 29.10]](/socr/uploads/math/0/0/3/003adcd7145f79d9a20472f7240aacfb.png)
- For α = 0.05, the 90%CI(μ) is constructed by:
![\overline{x}\pm 1.833{16\over \sqrt{10}}=14.77 \pm 1.645{16\over \sqrt{30}}=[12.83 ; 31.37]](/socr/uploads/math/7/2/7/727ea54232f72e56cd665abd35599d53.png)
- For α = 0.005, the 99%CI(μ) is constructed by:
![\overline{x}\pm 3.250{16\over \sqrt{10}}=14.77 \pm 2.575{16\over \sqrt{30}}=[5.66 ; 38.54]](/socr/uploads/math/a/a/2/aa21c039e631ea35f5a9f80be6c8165b.png)
Notice the increase of the CI's (directly related to the decrease of α) reflecting our choice for higher confidence.
Unknown variance
Suppose that we do not know the variance for the number of sentences per advertisement but use the sample variance 737.88 as an estimate (so the sample standard deviation is 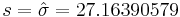 ).
).
- For α = 0.1, the 80%CI(μ) is constructed by:
![\overline{x}\pm 1.383{27.16390579\over \sqrt{10}}=14.77 \pm 1.28{16\over \sqrt{30}}=[10.22 ; 33.98]](/socr/uploads/math/2/4/5/2452b23296a089f83fb0070e6577aaf5.png)
- For α = 0.05, the 90%CI(μ) is constructed by:
![\overline{x}\pm 1.833{27.16390579\over \sqrt{10}}=14.77 \pm 1.645{16\over \sqrt{30}}=[6.35 ; 37.85]](/socr/uploads/math/3/5/3/353b1e85c8513acb0dd4a1cc9c769f0e.png)
- For α = 0.005, the 99%CI(μ) is constructed by:
![\overline{x}\pm 3.250{27.16390579 \over \sqrt{10}}=14.77 \pm 2.575{16\over \sqrt{30}}=[-5.82 ; 50.02]](/socr/uploads/math/5/9/2/5925bfd77f6bb8356af76bd481550091.png)
Notice the increase of the CI's (directly related to the decrease of α) reflecting our choice for higher confidence.
Hands-on activities
- See the SOCR Confidence Interval Experiment.
- Sample statistics, like the sample-mean and the sample-variance, may be easily obtained using SOCR Charts. The images below illustrate this functionality (based on the Bar-Chart and Index-Chart) using the 30 observations of the number of sentences per advertisement, reported above.
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: