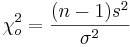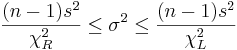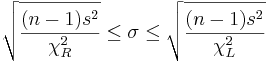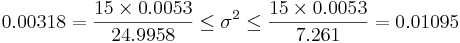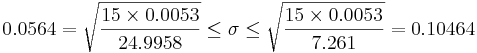AP Statistics Curriculum 2007 Estim Var
From Socr
(→Hands-on activities) |
m (→Point Estimates of Population Variance and Standard Deviation) |
||
| (6 intermediate revisions not shown) | |||
| Line 4: | Line 4: | ||
=== Point Estimates of Population Variance and Standard Deviation=== | === Point Estimates of Population Variance and Standard Deviation=== | ||
| - | The most unbiased point estimate for the population variance <math>\sigma^2</math> is the [[AP_Statistics_Curriculum_2007_EDA_Var | | + | The most unbiased point estimate for the population variance <math>\sigma^2</math> is the [[AP_Statistics_Curriculum_2007_EDA_Var | Sample-Variance (s<sup>2</sup>)]] and the point estimate for the population standard deviation <math>\sigma</math> is the [[AP_Statistics_Curriculum_2007_EDA_Var | Sample Standard Deviation (s)]]. |
| - | We use a [http://en.wikipedia.org/wiki/Chi_square_distribution Chi- | + | We use a [http://en.wikipedia.org/wiki/Chi_square_distribution Chi-Square Distribution] to construct confidence intervals for the variance and standard distribution. If the process or phenomenon we study generates a Normal random variable, then computing the following random variable (for a sample of size <math>n>1</math>) has a [[AP_Statistics_Curriculum_2007_Chi-Square|Chi-Square Distribution]] |
: <math>\chi_o^2 = {(n-1)s^2 \over \sigma^2}</math> | : <math>\chi_o^2 = {(n-1)s^2 \over \sigma^2}</math> | ||
| - | ===Chi- | + | ===Chi-Square Distribution Properties=== |
* All chi-squares values <math>\chi_o^2 \geq 0</math>. | * All chi-squares values <math>\chi_o^2 \geq 0</math>. | ||
| - | * The chi-square distribution is a family of curves, each determined by the degrees of freedom (n-1). See the interactive [http://socr.ucla.edu/htmls/SOCR_Distributions.html Chi-Square distribution]. | + | * The chi-square distribution is a family of curves, each is determined by the degrees of freedom (n-1). See the interactive [http://socr.ucla.edu/htmls/SOCR_Distributions.html Chi-Square distribution]. |
* To form a confidence interval for the variance (<math>\sigma^2</math>), use the <math>\chi^2(df=n-1)</math> distribution with degrees of freedom equal to one less than the sample size. | * To form a confidence interval for the variance (<math>\sigma^2</math>), use the <math>\chi^2(df=n-1)</math> distribution with degrees of freedom equal to one less than the sample size. | ||
| - | * The area under each curve of the Chi- | + | * The area under each curve of the Chi-Square Distribution equals one. |
| - | * All Chi- | + | * All Chi-Square Distributions are positively skewed. |
<center>[[Image:SOCR_EBook_Dinov_Estim_Var_020408_Fig1.jpg|500px]]</center> | <center>[[Image:SOCR_EBook_Dinov_Estim_Var_020408_Fig1.jpg|500px]]</center> | ||
| - | ===Interval Estimates of | + | ===Interval Estimates of Population Variance and Standard Deviation=== |
| - | Notice that the Chi- | + | Notice that the Chi-Square Distribution is '''not''' symmetric (positively skewed) and therefore, there are two critical values for each level of confidence. The value <math>\chi_L^2</math> represents the left-tail critical value and <math>\chi_R^2</math> represents the right-tail critical value. For various degrees of freedom and areas, you can compute all critical values either using the [http://socr.ucla.edu/htmls/SOCR_Distributions.html SOCR Distributions] or using the [http://socr.ucla.edu/Applets.dir/Normal_T_Chi2_F_Tables.htm SOCR Chi-square Distribution Calculator]. |
| - | * Example: Find the critical values, <math>\chi_L^2</math> and <math>\chi_R^2</math>, for a | + | * Example: Find the critical values, <math>\chi_L^2</math> and <math>\chi_R^2</math>, for a 90% confidence interval when the sample size is 25. Use the following Protocol: |
| - | ** Identify the degrees of freedom (<math>df=n-1=24</math>) and the level of confidence (<math>{\alpha\over 2}=0. | + | ** Identify the degrees of freedom (<math>df=n-1=24</math>) and the level of confidence (<math>{\alpha\over 2}=0.05</math>). |
** Find the left and right critical values, <math>\chi_L^2=13.848</math> and <math>\chi_R^2=36.415</math>, as in the image below. | ** Find the left and right critical values, <math>\chi_L^2=13.848</math> and <math>\chi_R^2=36.415</math>, as in the image below. | ||
<center>[[Image:SOCR_EBook_Dinov_Estim_Var_020408_Fig2.jpg|500px]]</center> | <center>[[Image:SOCR_EBook_Dinov_Estim_Var_020408_Fig2.jpg|500px]]</center> | ||
| - | ====Confidence | + | ====Confidence Interval for <math>\sigma^2</math>==== |
: <math>{(n-1)s^2 \over \chi_R^2} \leq \sigma^2 \leq {(n-1)s^2 \over \chi_L^2}</math> | : <math>{(n-1)s^2 \over \chi_R^2} \leq \sigma^2 \leq {(n-1)s^2 \over \chi_L^2}</math> | ||
| - | ====Confidence | + | ====Confidence Interval for <math>\sigma</math>==== |
: <math>\sqrt{(n-1)s^2 \over \chi_R^2} \leq \sigma \leq \sqrt{(n-1)s^2 \over \chi_L^2}</math> | : <math>\sqrt{(n-1)s^2 \over \chi_R^2} \leq \sigma \leq \sqrt{(n-1)s^2 \over \chi_L^2}</math> | ||
| - | ===Hands-on | + | ===Hands-on Activities=== |
* Construct the confidence intervals for <math>\sigma^2</math> and <math>\sigma</math> assuming the observations below represent a random sample from the liquid content (in fluid ounces) of 16 beverage cans and can be considered as Normally distributed. Use a 90% level of confidence. | * Construct the confidence intervals for <math>\sigma^2</math> and <math>\sigma</math> assuming the observations below represent a random sample from the liquid content (in fluid ounces) of 16 beverage cans and can be considered as Normally distributed. Use a 90% level of confidence. | ||
<center> | <center> | ||
| Line 53: | Line 53: | ||
: <math>0.0564=\sqrt{15\times 0.0053 \over 24.9958} \leq \sigma \leq \sqrt{15\times 0.0053 \over 7.261}=0.10464</math> | : <math>0.0564=\sqrt{15\times 0.0053 \over 24.9958} \leq \sigma \leq \sqrt{15\times 0.0053 \over 7.261}=0.10464</math> | ||
| - | ===More | + | ===More Examples=== |
| - | * You randomly select and measure the contents of 15 bottles of cough syrup. The results (in fluid ounces) are shown. Use a 95% level of confidence to construct a confidence interval for the standard deviation (<math>\sigma</math>) assuming the contents of these cough syrup bottles | + | * You randomly select and measure the contents of 15 bottles of cough syrup. The results (in fluid ounces) are shown. Use a 95% level of confidence to construct a confidence interval for the standard deviation (<math>\sigma</math>) assuming the contents of these cough syrup bottles are Normally distributed. Does this CI(<math>\sigma</math>) suggest that the variation in the bottles is at an acceptable level if the '''population standard deviation''' of the bottle’s contents should be less than 0.025 fluid ounce? |
<center> | <center> | ||
{| class="wikitable" style="text-align:center; width:75%" border="1" | {| class="wikitable" style="text-align:center; width:75%" border="1" | ||
| Line 66: | Line 66: | ||
* For the [[SOCR_012708_ID_Data_HotDogs | hot-dogs dataset]] construct 97% CI for the population standard deviation of the calorie and sodium contents, separately. | * For the [[SOCR_012708_ID_Data_HotDogs | hot-dogs dataset]] construct 97% CI for the population standard deviation of the calorie and sodium contents, separately. | ||
| + | |||
| + | * [[SOCR_EduMaterials_Activities_General_CI_Experiment | Also see the General Confidence Interval Activity]]. | ||
<hr> | <hr> | ||
| - | === | + | ===[[EBook_Problems_Estim_Var|Problems]]=== |
<hr> | <hr> | ||
Current revision as of 16:49, 27 February 2012
Contents |
General Advance-Placement (AP) Statistics Curriculum - Estimating Population Variance
In manufacturing, and many other fields, controlling the amount of variance in producing machinery parts is very important. It is important that the parts vary little or not at all.
Point Estimates of Population Variance and Standard Deviation
The most unbiased point estimate for the population variance σ2 is the Sample-Variance (s2) and the point estimate for the population standard deviation σ is the Sample Standard Deviation (s).
We use a Chi-Square Distribution to construct confidence intervals for the variance and standard distribution. If the process or phenomenon we study generates a Normal random variable, then computing the following random variable (for a sample of size n > 1) has a Chi-Square Distribution
Chi-Square Distribution Properties
- All chi-squares values
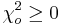 .
.
- The chi-square distribution is a family of curves, each is determined by the degrees of freedom (n-1). See the interactive Chi-Square distribution.
- To form a confidence interval for the variance (σ2), use the χ2(df = n − 1) distribution with degrees of freedom equal to one less than the sample size.
- The area under each curve of the Chi-Square Distribution equals one.
- All Chi-Square Distributions are positively skewed.
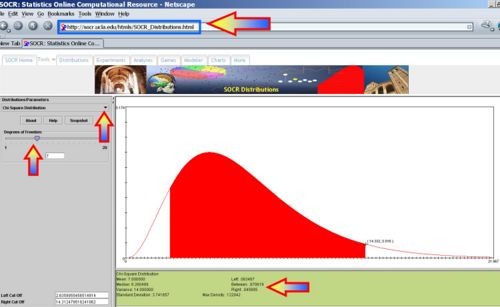
Interval Estimates of Population Variance and Standard Deviation
Notice that the Chi-Square Distribution is not symmetric (positively skewed) and therefore, there are two critical values for each level of confidence. The value  represents the left-tail critical value and
represents the left-tail critical value and 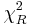 represents the right-tail critical value. For various degrees of freedom and areas, you can compute all critical values either using the SOCR Distributions or using the SOCR Chi-square Distribution Calculator.
represents the right-tail critical value. For various degrees of freedom and areas, you can compute all critical values either using the SOCR Distributions or using the SOCR Chi-square Distribution Calculator.
- Example: Find the critical values,
 and
and 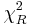 , for a 90% confidence interval when the sample size is 25. Use the following Protocol:
, for a 90% confidence interval when the sample size is 25. Use the following Protocol:
- Identify the degrees of freedom (df = n − 1 = 24) and the level of confidence (
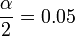 ).
).
- Find the left and right critical values,
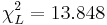 and
and 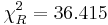 , as in the image below.
, as in the image below.
- Identify the degrees of freedom (df = n − 1 = 24) and the level of confidence (

Confidence Interval for σ2
Confidence Interval for σ
Hands-on Activities
- Construct the confidence intervals for σ2 and σ assuming the observations below represent a random sample from the liquid content (in fluid ounces) of 16 beverage cans and can be considered as Normally distributed. Use a 90% level of confidence.
| 14.816 | 14.863 | 14.814 | 14.998 | 14.965 | 14.824 | 14.884 | 14.838 | 14.916 | 15.021 | 14.874 | 14.856 | 14.860 | 14.772 | 14.980 | 14.919 |
- Get the sample statistics from SOCR Charts (e.g., Index Plot); Sample-Mean=14.8875; Sample-SD=0.072700298, Sample-Var=0.005285333.
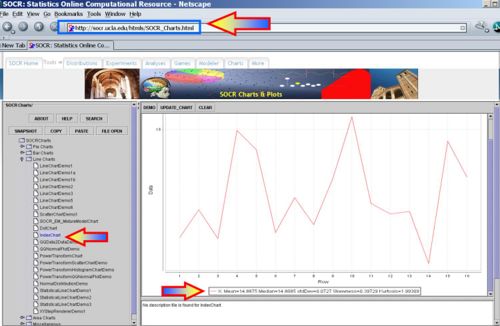
- Identify the degrees of freedom (df = n − 1 = 15) and the level of confidence (α / 2 = 0.05), as we are looking for a (1 − α)100%CI(σ2).
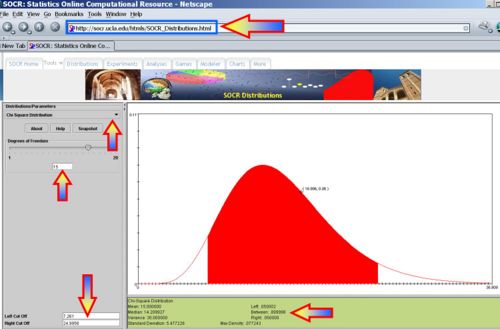
- Find the left and right critical values,
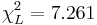 and
and 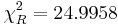 using SOCR Chi-Square Distribution, as in the image below.
using SOCR Chi-Square Distribution, as in the image below.
- CI(σ2)
- CI(σ)
More Examples
- You randomly select and measure the contents of 15 bottles of cough syrup. The results (in fluid ounces) are shown. Use a 95% level of confidence to construct a confidence interval for the standard deviation (σ) assuming the contents of these cough syrup bottles are Normally distributed. Does this CI(σ) suggest that the variation in the bottles is at an acceptable level if the population standard deviation of the bottle’s contents should be less than 0.025 fluid ounce?
| 4.211 | 4.246 | 4.269 | 4.241 | 4.260 | 4.293 | 4.189 | 4.248 | 4.220 | 4.239 | 4.253 | 4.209 | 4.300 | 4.256 | 4.290 |
- The gray whale has the longest annual migration distance of any mammal. Gray whales leave Baja, California, and western Mexico in the spring, migrating to the Bering and Chukchi seas for the summer months. Tracking a sample of 50 whales for a year provided a mean migration distance of 11,064 miles with a standard deviation of 860 miles. Construct a 90% confidence interval for the variance for the migrating whales. Assume that the population of migration distances is Normally distributed.
- For the hot-dogs dataset construct 97% CI for the population standard deviation of the calorie and sodium contents, separately.
Problems
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: