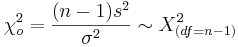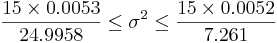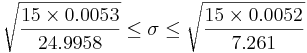AP Statistics Curriculum 2007 Hypothesis Var
From Socr
Contents |
General Advance-Placement (AP) Statistics Curriculum - Testing a Claim about a Standard Deviation or Variance
Assessing the amount of variation in a process, natural phenomenon or an experiment is of paramount importance in many fields. For instance, a computer manufacturer may dismiss a batch of computer chips if they vary more than certain tollerance levels in their clock-speed, heat emmissions or energy consumptions.
Background
Recall that the sample-variance (s2) is an unbiased point estimate for the population variance σ2, and similarly, the sample-standard-deviation (s) is a good point estimate for the population-standard-deviation σ.
The sample-variance is roughly Chi-square distributed:
Testing a Claim about the Variance (σ2)
For Normally distributed random variables, given 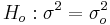 vs.
vs. 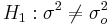 , then
, then 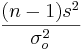 has a
has a 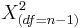 distribution, where s2 is the sample variance.
distribution, where s2 is the sample variance.
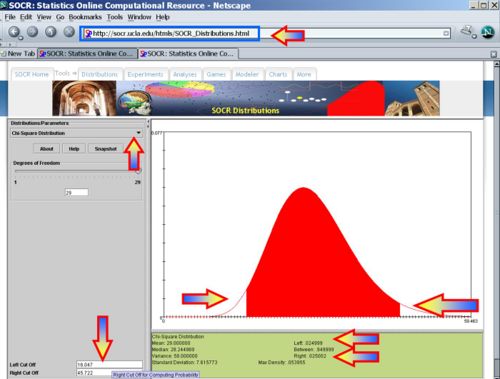
Notice that the Chi-square distribution is not symmetric (it is positively skewed) and therefore, there are two critical values for each level of confidence (1 − α). The value  represents the left-tail critical value and
represents the left-tail critical value and 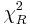 represents the right-tail critical value. For various degrees of freedom and areas, you can compute all critical values either using the SOCR Chi-Square Distribution or using the SOCR Chi-square distribution calculator.
represents the right-tail critical value. For various degrees of freedom and areas, you can compute all critical values either using the SOCR Chi-Square Distribution or using the SOCR Chi-square distribution calculator.
- Example: A random sample of size 30 drawn from a Normal distribution has sample-variance s2 = 5. Test at the α = 0.05 level of significance if this is consistent with Ho:σ2 = 2.
- Test statistic:
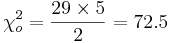 .
.
- Left and Right Chi-Square critical values (for α = 0.05) are
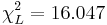 and
and 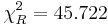 . Since,
. Since, 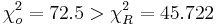 , Ho is rejected at the α = 0.05 level of significance.
, Ho is rejected at the α = 0.05 level of significance.
Testing a Claim about the Standard Deviation (σ)
As the standard deviation is just th square root of the variance (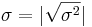 ), we do significance testing for the standard deviation anologously.
), we do significance testing for the standard deviation anologously.
For Normally distributed random variables, given Ho:σ = σo vs. 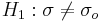 , then
, then 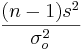 has a
has a 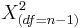 distribution, where s2 is the square of the sample standard deviation.
distribution, where s2 is the square of the sample standard deviation.
Hands-on activities
- Formulate appropriate hypothesis and assess the significance of the evidence to reject the null hypothesis for the population standard deviation (σ) assuming the observations below represent a random sample from the liquid content (in fluid ounces) of 16 beverage cans and can be considered as Normally distributed. Use a 90% level of confidence (α = 0.1).
| 14.816 | 14.863 | 14.814 | 14.998 | 14.965 | 14.824 | 14.884 | 14.838 | 14.916 | 15.021 | 14.874 | 14.856 | 14.860 | 14.772 | 14.980 | 14.919 |
- Hypotheses: Ho:σ = 0.04 vs.
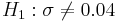 .
.
- Get the sample statistics from SOCR Charts (e.g., Index Plot); Sample-Mean=14.8875; Sample-SD=0.072700298, Sample-Var=0.005285333.
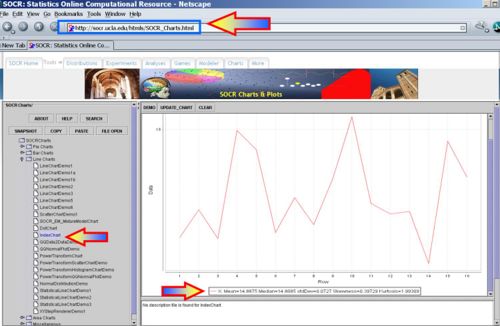
- Identify the degrees of freedom (df = n − 1 = 15) and the level of confidence (
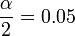 , as we are looking for a (1 − α)100%CI(σ)).
, as we are looking for a (1 − α)100%CI(σ)).
- Find the left and right critical values,
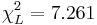 and
and 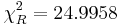 , as in the image below.
, as in the image below.
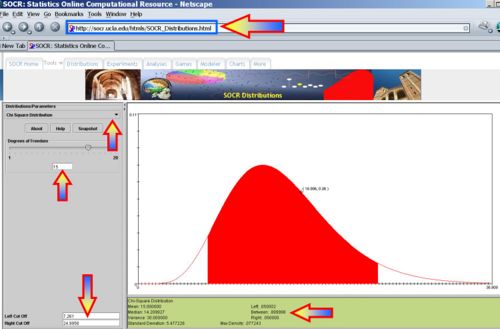
- CI(σ2)
- CI(σ)
More examples
- You randomly select and measure the contents of 15 bottles of cough syrup. The results (in fluid ounces) are shown. Use a 95% level of confidence to construct a confidence interval for the standard deviation (σ) assuming the contents of these cough syrup bottles is Normally distributed. Does this CI(σ) suggest that the variation in the bottles is at an acceptable level if the population standard deviation of the bottle’s contents should be less than 0.025 fluid ounce?
| 4.211 | 4.246 | 4.269 | 4.241 | 4.260 | 4.293 | 4.189 | 4.248 | 4.220 | 4.239 | 4.253 | 4.209 | 4.300 | 4.256 | 4.290 |
- The gray whale has the longest annual migration distance of any mammal. Gray whales leave Baja, California, and western Mexico in the spring, migrating to the Bering and Chukchi seas for the summer months. Tracking a sample of 50 whales for a year provided a mean migration distance of 11,064 miles with a standard deviation of 860 miles. Construct a 90% confidence interval for the variance for the migrating whales. Assume that the population of migration distances is Normally distributed.
- For the hot-dogs dataset construct 97% CI for the population standard deviation of the calorie and sodium contents, separately.
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: