AP Statistics Curriculum 2007 IntroTools
From Socr
(→Hands-on Examples & Activities) |
|||
| Line 55: | Line 55: | ||
* Now we can demonstrate the use of [http://www.socr.ucla.edu/htmls/SOCR_Analyses.html SOCR Analyses] to look for Left-Right hemispheric (HEMISPHERE) effects of the average MRI intensities (MEAN) in one Region of Interest (Occipital lobe, ROI=2). For this we can apply simple linear regression analysis. This is justified as the average intensities will follow [[About_pages_for_SOCR_Distributions |Normal Distribution]] by the [[SOCR_EduMaterials_Activities_GeneralCentralLimitTheorem | Central Limit Theorem]]. | * Now we can demonstrate the use of [http://www.socr.ucla.edu/htmls/SOCR_Analyses.html SOCR Analyses] to look for Left-Right hemispheric (HEMISPHERE) effects of the average MRI intensities (MEAN) in one Region of Interest (Occipital lobe, ROI=2). For this we can apply simple linear regression analysis. This is justified as the average intensities will follow [[About_pages_for_SOCR_Distributions |Normal Distribution]] by the [[SOCR_EduMaterials_Activities_GeneralCentralLimitTheorem | Central Limit Theorem]]. | ||
| - | * Copy in your mouse buffer the 6<sup>th</sup> (MEAN), 8<sup>th</sup> (HEMISPHERE) and 9<sup>th</sup> (ROI) columns of the [http://www.stat.ucla.edu/~dinov/courses_students.dir/04/Spring/Stat233.dir/HWs.dir/AD_NeuroPsychImagingData1.html following data table]. You can paste these three columns in Excel or any other spreadsheet program and reorder the rows first by ROI and then by HEMISPHERE. This will give you 240 rows of measurements (MEAN) for ROI=2 (Occipital lobe). The break down of this number is as follows 240 = 2(hemispheres) * 3 (tissue types) * 40 (subjects). | + | * Copy in your mouse buffer the 6<sup>th</sup> (MEAN), 8<sup>th</sup> (HEMISPHERE) and 9<sup>th</sup> (ROI) columns of the [http://www.stat.ucla.edu/~dinov/courses_students.dir/04/Spring/Stat233.dir/HWs.dir/AD_NeuroPsychImagingData1.html following data table]. You can paste these three columns in Excel or any other spreadsheet program and reorder the rows first by ROI and then by HEMISPHERE. This will give you [[AP_Statistics_Curriculum_2007_IntroTools_Data | 240 rows of measurements]] (MEAN) for ROI=2 (Occipital lobe). The break down of this number is as follows 240 = 2(hemispheres) * 3 (tissue types) * 40 (subjects). |
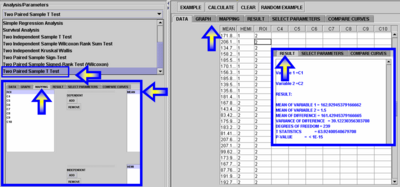
* Copy these 240 Rows and paste them in the Paired T-test Analysis under [http://www.socr.ucla.edu/htmls/SOCR_Analyses.html SOCR Analyses]. Map the MEAN and HEMISPHERE columes to Dependent and Independent variables and then click '''Calculate'''. The results indicate that there were significant differences between the Left and Right Occipital mean intensities for these 40 subjects. | * Copy these 240 Rows and paste them in the Paired T-test Analysis under [http://www.socr.ucla.edu/htmls/SOCR_Analyses.html SOCR Analyses]. Map the MEAN and HEMISPHERE columes to Dependent and Independent variables and then click '''Calculate'''. The results indicate that there were significant differences between the Left and Right Occipital mean intensities for these 40 subjects. | ||
Revision as of 16:38, 20 June 2007
Contents |
General Advance-Placement (AP) Statistics Curriculum - Statistics with Tools
Statistics with Tools (Calculators and Computers)
A critical component in any data analysis or process understanding protocol is that one needs to develop a model that has a compact analytical representation (e.g., formulas, symbolic equations, etc.) The model is used to study the process theoretically. Emperical validation of the model is carried by pluggin in data and actually testing the model. This validation stop may be done manually by computing the model prediction or model inference from recorded measurements. This typically may be done by hand only for small number of observations (<10). In practice, most of the time, we use or write algorithms and computer programs that automate these calculations for better efficiency, accuracy and consistency in applying the model to larger datasets.
There are a number of statistical software tools (programs) that one can employ for data analysis and statistical processing. Some of these are: SAS, SYSTAT, SPSS, R, SOCR.
Approach & Model Validation
Before any statistical analysis tool is employed to analyze a dataset, one needs to carefully review the prerequisites and assumptions that this model demands about the data and study design.
For example, if we measure the weight and height of students and want to study gender, age or race differences or association between weight and height, we need to make sure our sample size is large enough, these weight and height measurements are random (i.e., we do not have repeated measurements of the same student or twin-measurements) and that the students we can measure are a representative sample of the population that we are making inference about (e.g., 8th-grade students).
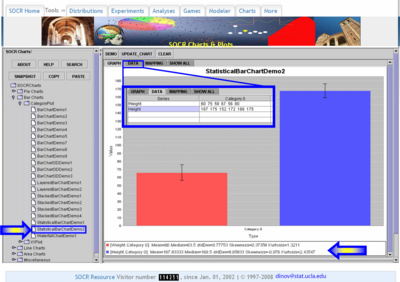
In this example, suppose we record the following 6 pairs of {weight (kg), height (cm)}:
| Student Index | 1 | 2 | 3 | 4 | 5 | 6 |
| Weight | 60 | 75 | 58 | 67 | 56 | 80 |
| Height | 167 | 175 | 152 | 172 | 166 | 175 |
We can easily compute the average weight (66 kg) and height (167 cm) using the sample mean-formula. We can also compute these averages using the SOCR Charts, or any other statistical package, as shown in the image below.
Computational Resources: Internet-based SOCR Tools
Several of the SOCR tools and resources will be shown later to be useful in a variety of sitiations. Here is just a list of these with one example of each:
- SOCR Charts and Histogram Charts Activity
- SOCR Analyses and Simple Linear Regression Activity
- SOCR Modeler and Random Number Generation Activity
Hands-on Examples & Activities
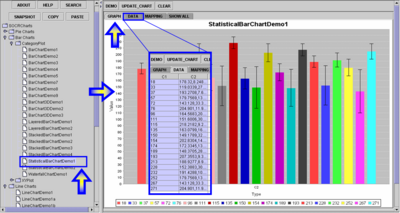
- As part of a brain imaging study of Alzheimer's disease *, the investigators collected the following data.
- Let's try to plot some of this data first
- Now we can demonstrate the use of SOCR Analyses to look for Left-Right hemispheric (HEMISPHERE) effects of the average MRI intensities (MEAN) in one Region of Interest (Occipital lobe, ROI=2). For this we can apply simple linear regression analysis. This is justified as the average intensities will follow Normal Distribution by the Central Limit Theorem.
- Copy in your mouse buffer the 6th (MEAN), 8th (HEMISPHERE) and 9th (ROI) columns of the following data table. You can paste these three columns in Excel or any other spreadsheet program and reorder the rows first by ROI and then by HEMISPHERE. This will give you 240 rows of measurements (MEAN) for ROI=2 (Occipital lobe). The break down of this number is as follows 240 = 2(hemispheres) * 3 (tissue types) * 40 (subjects).
- Copy these 240 Rows and paste them in the Paired T-test Analysis under SOCR Analyses. Map the MEAN and HEMISPHERE columes to Dependent and Independent variables and then click Calculate. The results indicate that there were significant differences between the Left and Right Occipital mean intensities for these 40 subjects.
References
- Mega MS, Dinov, ID, Thompson, P, Manese, M, Lindshield, C, Moussai, J, Tran, N, Olsen, K, Felix, J, Zoumalan, C, Woods, RP, Toga, AW, Mazziotta, JC. Automated Brain Tissue Assessment in the Elderly and Demented Population: Construction and Validation of a Sub-Volume Probabilistic Brain Atlas, NeuroImage, 26(4), 1009-1018, 2005.
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
