AP Statistics Curriculum 2007 Normal Std
From Socr
| Line 1: | Line 1: | ||
| - | == | + | ====A Game of Chance==== |
| + | * Suppose we are offered to play a game of chance under these conditions: it costs us to play $1.50 and the awarded prices are {$1, $2, $3}. Assume the probabilities of winning each price are {0.6, 0.3, 0.1}, respectively. Should we play the game? What are our chances of winning/loosing? Let's let X=awarded price. Then X={1, 2, 3}. | ||
| - | === Standard Normal | + | <center> |
| + | {| class="wikitable" style="text-align:center; width:75%" border="1" | ||
| + | |- | ||
| + | | x || 1 || 2 || 3 | ||
| + | |- | ||
| + | | P(X=x) || 0.6 || 0.3 || 0.1 | ||
| + | |- | ||
| + | | x*P(X=x) || 0.6 || 0.6 || 0.3 | ||
| + | |} | ||
| + | </center> | ||
| + | Then the mean of this game (i.e., expected return or expectation) is computed as the weighted (by the outcome probabilities) average of all the outcome prices: <math>E[X] = x_1P(X=x_1) + x_2P(X=x_2)+x_3P(X=x_3) = 1\times 0.6 + 2\times 0.3 + 3\times 0.1 = 1.5</math>. In other words, the expected return of this came is $1.5, which equals the entry fee, and hence the game is fair - neither the player nor the house has an advantage in this game (on the long run!) Of course, each streak of n games will produce different outcomes and may give small advantage to one side, however, on the long run, no one will make money. | ||
| + | |||
| + | The variance for this game is computed by <math>VAR[X] = (x_1-1.5)^2P(X=x_1) + (x_2-1.5)^2P(X=x_2)+(x_3-1.5)^2P(X=x_3) = </math> | ||
| + | <math>=0.25\times 0.6 + 0.25\times 0.3 + 2.25\times 0.1 = 0.45</math>. Thus, the standard deviation is <math>SD[X] = \sqrt{VAR[X]}=0.67</math>. | ||
| + | |||
| + | * Suppose now we ''alter the rules for the game of chance'' and the new pay-off is as follows: | ||
| + | <center> | ||
| + | {| class="wikitable" style="text-align:center; width:75%" border="1" | ||
| + | |- | ||
| + | | x || 0 || 1.5 || 3 | ||
| + | |- | ||
| + | | P(X=x) || 0.6 || 0.3 || 0.1 | ||
| + | |- | ||
| + | | x*P(X=x) || 0 || 0.45 || 0.3 | ||
| + | |} | ||
| + | </center> | ||
| + | |||
| + | ** What is the ''new expected return'' of the game? Remember, the old expectation was equal to the entrance fee of $1.50, and the game was fair! | ||
| + | ** The change in the pay-off of the game may be represented by this linear transformation <math>Y = {3(X-1)\over 2}</math>. Therefore, by our rules for computing expectations of linear functions, <math>E[Y] = 3/2 E(X) –3/2 = 3/4 = 0.75</math>, and the game became clearly biased. Note how easy it is to compute ''E[Y]'', using this formula. At the same time, we could have computed the expectation of ''Y'' using first-principles (adding the values of the last row in the revised table above)! | ||
| + | |||
| + | * You can play similar games under different conditions for the probability distribution of the prices using the SOCR [[SOCR_EduMaterials_Activities_BinomialCoinExperiment | Binomial Coin]] or [[SOCR_EduMaterials_Activities_DiceExperiment | Die]] experiments. ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Standard Normal Variables and Experiments== | ||
| + | |||
| + | === Standard Normal Distribution=== | ||
The standard normal distribution is a continuous distribution where the following exact ''areas'' are bound between the Standard Normal Density function and the x-axis on the symmetric intervals around the origin: | The standard normal distribution is a continuous distribution where the following exact ''areas'' are bound between the Standard Normal Density function and the x-axis on the symmetric intervals around the origin: | ||
* The area: -1 < z < 1 = 0.8413 - 0.1587 = 0.6826 | * The area: -1 < z < 1 = 0.8413 - 0.1587 = 0.6826 | ||
| Line 13: | Line 46: | ||
===Experiments=== | ===Experiments=== | ||
| - | Suppose we decide to test the state of 100 used batteries. To do that, we | + | Suppose we decide to test the state of 100 used batteries. To do that, we connect each battery to a volt-meter by randomly attaching the positive (+) and negative (-) battery terminals to the corresponding volt-meter's connections. Electrical current always flows from + to -, i.e., the current goes in the direction of the voltage drop. Depending upon which way the battery is connected to the volt-meter we can observe positive or negative voltage recordings (voltage is just a difference, which forces current to flow from higher to the lower voltage.) Denote <math>X_i</math>={measured voltage for battery i} - this is random variable 0 and assume the distribution of all <math>X_i</math> is Standard Normal, <math>X_i \sim N(0,1)</math>. Use the Normal Distribution (with mean=0 and variance=1) in the [http://socr.ucla.edu/htmls/SOCR_Distributions.html SOCR Distribution applet] to address the following questions. This [[Help_pages_for_SOCR_Distributions | Distributions help-page may be useful in understanding SOCR Distribution Applet]]. How many batteries, from the sample of 100, can we expect to have? |
* Absolute Voltage > 1? P(X>1) = 0.1586, thus we expect 15-16 batteries to have voltage exceeding 1. | * Absolute Voltage > 1? P(X>1) = 0.1586, thus we expect 15-16 batteries to have voltage exceeding 1. | ||
<center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig1.jpg|500px]]</center> | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig1.jpg|500px]]</center> | ||
Revision as of 20:16, 31 January 2008
Contents |
A Game of Chance
- Suppose we are offered to play a game of chance under these conditions: it costs us to play $1.50 and the awarded prices are {$1, $2, $3}. Assume the probabilities of winning each price are {0.6, 0.3, 0.1}, respectively. Should we play the game? What are our chances of winning/loosing? Let's let X=awarded price. Then X={1, 2, 3}.
| x | 1 | 2 | 3 |
| P(X=x) | 0.6 | 0.3 | 0.1 |
| x*P(X=x) | 0.6 | 0.6 | 0.3 |
Then the mean of this game (i.e., expected return or expectation) is computed as the weighted (by the outcome probabilities) average of all the outcome prices: ![E[X] = x_1P(X=x_1) + x_2P(X=x_2)+x_3P(X=x_3) = 1\times 0.6 + 2\times 0.3 + 3\times 0.1 = 1.5](/socr/uploads/math/0/b/c/0bcfa9cb8cff091987dd0d382c724b8e.png) . In other words, the expected return of this came is $1.5, which equals the entry fee, and hence the game is fair - neither the player nor the house has an advantage in this game (on the long run!) Of course, each streak of n games will produce different outcomes and may give small advantage to one side, however, on the long run, no one will make money.
. In other words, the expected return of this came is $1.5, which equals the entry fee, and hence the game is fair - neither the player nor the house has an advantage in this game (on the long run!) Of course, each streak of n games will produce different outcomes and may give small advantage to one side, however, on the long run, no one will make money.
The variance for this game is computed by VAR[X] = (x1 − 1.5)2P(X = x1) + (x2 − 1.5)2P(X = x2) + (x3 − 1.5)2P(X = x3) =
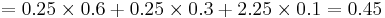 . Thus, the standard deviation is
. Thus, the standard deviation is ![SD[X] = \sqrt{VAR[X]}=0.67](/socr/uploads/math/2/b/c/2bc8ebb78cb6a8a87695ec1a37106d60.png) .
.
- Suppose now we alter the rules for the game of chance and the new pay-off is as follows:
| x | 0 | 1.5 | 3 |
| P(X=x) | 0.6 | 0.3 | 0.1 |
| x*P(X=x) | 0 | 0.45 | 0.3 |
- What is the new expected return of the game? Remember, the old expectation was equal to the entrance fee of $1.50, and the game was fair!
- The change in the pay-off of the game may be represented by this linear transformation
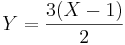 . Therefore, by our rules for computing expectations of linear functions, Failed to parse (lexing error): E[Y] = 3/2 E(X) –3/2 = 3/4 = 0.75
. Therefore, by our rules for computing expectations of linear functions, Failed to parse (lexing error): E[Y] = 3/2 E(X) –3/2 = 3/4 = 0.75
, and the game became clearly biased. Note how easy it is to compute E[Y], using this formula. At the same time, we could have computed the expectation of Y using first-principles (adding the values of the last row in the revised table above)!
- You can play similar games under different conditions for the probability distribution of the prices using the SOCR Binomial Coin or Die experiments. == General Advance-Placement (AP) Statistics Curriculum - Standard Normal Variables and Experiments==
Standard Normal Distribution
The standard normal distribution is a continuous distribution where the following exact areas are bound between the Standard Normal Density function and the x-axis on the symmetric intervals around the origin:
- The area: -1 < z < 1 = 0.8413 - 0.1587 = 0.6826
- The area: -2.0 < z < 2.0 = 0.9772 - 0.0228 = 0.9544
- The area: -3.0 < z < 3.0 = 0.9987 - 0.0013 = 0.9974

- Standard Normal density function
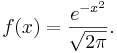
- The Standard Normal distribution is also a special case of the more general normal distribution where the mean is set to zero and a variance to one. The Standard Normal distribution is often called the bell curve because the graph of its probability density resembles a bell.
Experiments
Suppose we decide to test the state of 100 used batteries. To do that, we connect each battery to a volt-meter by randomly attaching the positive (+) and negative (-) battery terminals to the corresponding volt-meter's connections. Electrical current always flows from + to -, i.e., the current goes in the direction of the voltage drop. Depending upon which way the battery is connected to the volt-meter we can observe positive or negative voltage recordings (voltage is just a difference, which forces current to flow from higher to the lower voltage.) Denote Xi={measured voltage for battery i} - this is random variable 0 and assume the distribution of all Xi is Standard Normal, 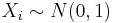 . Use the Normal Distribution (with mean=0 and variance=1) in the SOCR Distribution applet to address the following questions. This Distributions help-page may be useful in understanding SOCR Distribution Applet. How many batteries, from the sample of 100, can we expect to have?
. Use the Normal Distribution (with mean=0 and variance=1) in the SOCR Distribution applet to address the following questions. This Distributions help-page may be useful in understanding SOCR Distribution Applet. How many batteries, from the sample of 100, can we expect to have?
- Absolute Voltage > 1? P(X>1) = 0.1586, thus we expect 15-16 batteries to have voltage exceeding 1.
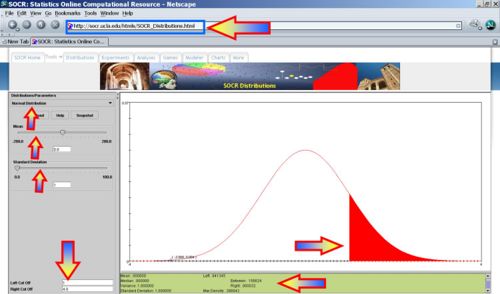
- |Absolute Voltage| > 1? P(|X|>1) = 1- 0.682689=0.3173, thus we expect 31-32 batteries to have absolute voltage exceeding 1.
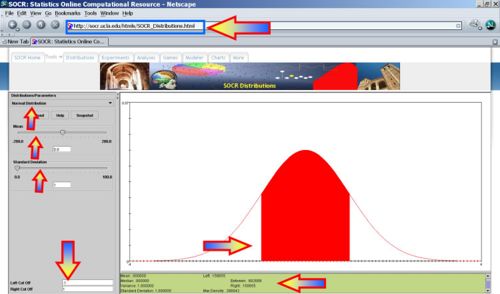
- Voltage < -2? P(X<-2) = 0.0227, thus we expect 2-3 batteries to have voltage less than -2.
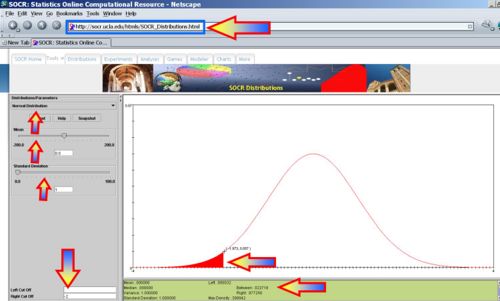
- Voltage <= -2? P(X<=-2) = 0.0227, thus we expect 2-3 batteries to have voltage less than or equal to -2.

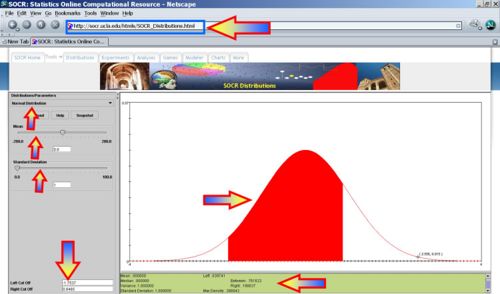
- -1.7537 < Voltage < 0.8465? P(-1.7537 < X < 0.8465) = 0.761622, thus we expect 76 batteries to have voltage in this range.
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
