SOCR EduMaterials Activities BallotExperiment
From Socr
Contents |
Ballot Experiment
Description
The ballot experiment involves candidate A receiving a votes and candidate B receiving b votes. Assuming randomly ordered votes, a must be greater than b. The event of interest is for A to be equal to or greater than B in the vote count. Graphically, the first diagram will illustrate the difference between the number of votes between A and B during the trials, thus it is always above the horizontal axis, except at the origin. The indicator variable I of every event is recorded on the left most table of the experiment. In the distribution graph, the probability density function of I is shown, as well as its recording in the distribution table on the right. The empirical density of I is illustrated in the second graph as red on each update and recorded in the second table.
Goals
To provide an insightful method for probability between two distinct events (e.g. A/B, weekday/weekend, chocolate/vanilla, etc.) and create a general perception about presumption and chance.
Experiment
Go to the SOCR Experiments and select the Ballot Experiment from the drop-down list of experiments on the top left. The image below shows the initial view of this experiment:
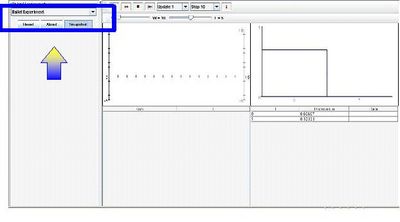
Parameters a and b can be modified by adjusting the two scrolls on top of the graphs, where W represents the number of trials won, and L represents the number of trials lost. Above the scrolls are two categories. The left denotes the number of trials that are to be executed when pressing the fast-forward symbol and the right denotes the number of trials to be carried out within an experiment. When pressing the play button, the experiment will run exactly one trial. The outcome is then displayed in the tables below, where 1 symbolizes success and 0 as failure. Selecting the fast-forward button will automatically update the experiment every 1, 10, 100, or 1000 trial as selected by the experimenter. It will then stop once it has reached 10, 100, 1000, or 10000 trials, or continue until the experimenter clicks on the stop symbol. The fourth represents a reset button in which it will clear all data and information of the current experiment. Lastly, the most right button, illustrated with an “I” informs users of the summary and main purpose of the ballot experiment.
When setting the parameter a and b where the distribution table (right) displays the probability outcome of 1 to be greater than 0, the probability density function will also graphically display the settings of the parameter in which 1 will be greater than 0.After many trials, the empirical density of I (red) will eventually ‘match’ the probability density function (blue), as shown in the figure below:
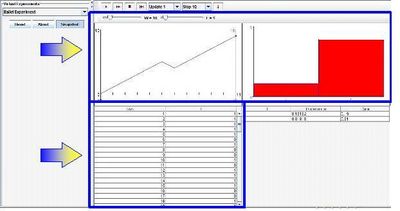
Similarly, when parameters are set in which the probability distribution of 0 is greater than 1, graphically, 0 will also be greater than 1. After many trials, the empirical density will begin to ‘match’ the probability density function.
All the trials are kept in record and it is helpful when executing large numbers of trials with no specified maximum number of runs.
Applications
This applet will not only develop a process to predict outcomes of ballots but it also relates to real life experiences. The following examples show its relativity to many different situations:
A constructor wants to determine what types of materials are suitable to develop a structure in a humid and windy environment. Using this applet may be of an assistance for him. The specific material strength for building will either break (failure) or not (success) after every hurricane (trial).
Experimenters are interested to know if consumers are more likely to purchase tropical fruits or seasonal fruits during summer. By using this applet, a success will represent the proportion of consumers who purchase tropical fruits during the summer and a failure as those who purchase seasonal fruits. At the end of the experiment, data may be analyzed and if it is accurate, it could be used as a generalization.
A manager wants to expand his company by opening another store in a new location. He is given two options of location: in the mall or at the corner in down town. He uses this java applet by recording the population of customers every other hour and comparing these values with each other. From the study, he determines that the corner in down town has a higher population than in the mall. He then concludes to open a new location in down town.
The SOCR Ballot Experiment allows us to simulate natural phenomena on the computer.
Translate this page:
