SOCR EduMaterials Activities LawOfLargeNumbers2
From Socr
SOCR Educational Materials - Activities - SOCR Law of Large Numbers Activity
This is part II of a heterogeneous activity that demonstrates the Law of Large Numbers (LLN). Part I of this activity contains the introductory materials.
The Law of Large Numbers
If an event of probability p is observed repeatedly during independent repetitions, the ratio of the observed frequency of that event to the total number of repetitions converges towards p as the number of repetitions becomes arbitrarily large.
Complete details about the LLN can be found here
Exercise 1
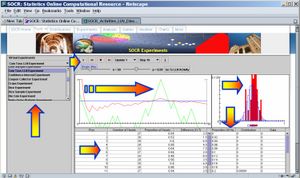
This exercise will demonstrate one special instance of the LLN. Here you will be able to toss a coin a number of times and instead of focusing on the actual outcomes of the experiment, we will be paying special attention to two random variables defined on the outcomes. The first variable will be the proportion of Heads and the second will be the differences of the number of Heads and Tails. This will empirically demonstrate the LLN and it's most common misconceptions (presented below). Point your browser to the SOCR Experiments and select the Coin Toss LLN Experiment from the drop-down list of experiments in the top-left panel. This applet consists of a control toolbar on the top with 2 graph panels in the middle and 2 results tables on the bottom. Use the toolbar to run one, or many, experiments, stop or reset an experiment. You may also select your sample size (n) and the probability of Heads (p) using the toolbar sliders. The left graph panel in the middle will dynamically plot the values of the two variables of interest (proportion of heads and difference of Heads and Tails). The right graphing panel will display the theoretical distribution and the sample histogram for this random experiment (for the proportion of Heads). One would expect to obtain a good match between these two distribution plots, as the number of experiments increases. The two tables on the bottom present the summaries of all trials of this experiment. From these tables, you can copy and paste the summaries for further processing using other computational resources (e.g., SOCR Modeler or MS Excel).
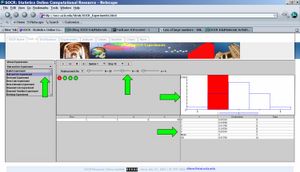
Now, select n=100 and p=0.5. The figure below shows a snapshot of the applet. Remember that each time you run the applet the random samples will be different and the figures and results will generally vary. Click on the Run/Step button to see the experiment run and observe the proportion of heads and differences evolve over time. The statement of the LLN in this experiment is simply that as the number of experiments increases the sample proportion of Heads (red curve) will approach the theoretical (user preset) value of p (in this case p=0.5). Change the values of n and p and run the experiment interactively several times. Notice the behavior of the graphs of the two variables we study. Try to pose and answer questions like these:
- If we set p=0.1, what sample-size (n) would imply approximately Normal distribution of the process (right graph needs to be unimodal, symmetric and bell-shaped)?
- Does the curve representing the differences of Heads and Tails (red curve) always diverge?
- What proportion of experiments (each of fixed sample-size, say n=40) is expected to have their sample proportions within 0.1 from the value of p?
Exercise 2
Go to the SOCR Experiments and select the Binomial Coin Experiment. Select the number of coins (n=3) and probability of heads (p=0.5). Notice the blue model distribution of the Number of Heads (X), in the right panel. Try varying the probability (p) and/or the number of coins (n) and see how these parameters affect the shape of this distribution. Can you make sense of it? For example, if p increases, why does the distribution move to the right and become concentrated at the right end (i.e., left-skewed)? And vice-versa, if you decrease the probability of a head, the distribution will become skewed to the right and centered in the left end of the range of X (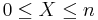 ).
).
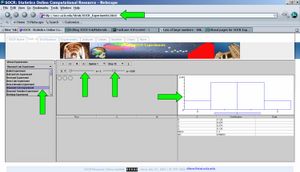
Let us toss three coins 10 times (by clicking 10 times on the RUN button of the applet on the top). We observe the sampling distribution of X, how many times did we observe 0, 1, 2 or 3 heads in the 10 experiments (each experiment involves tossing 3 coins independently) in red color superimposed to the theoretical (exact) distribution of X, in blue. The four panels in the middle of the Binomial Coin Applet show:
| Coin Box Panel, where all coin tosses are shown | The theoretical (blue) and sampling (observed, red) distributions of the Number of Heads in the series of 3-coin-toss experiments (X) |
| Summary statistics table that includes columns for the index of each Run, the Number of Heads and the Proportion of heads in each experiment | Numerical comparisons of the Theoretical and Sampling distribution (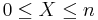 ) and two statistics (mean, SD) ) and two statistics (mean, SD)
|
Now take a snapshot of these results or store these summaries in the tables on the bottom.
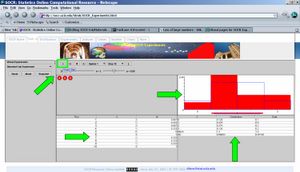
According to the LLN, if we were to increase the number of coins we tossed at each experiments, say from n=3 to n=9, we need to get a better fit between theoretical and sampling distributions. Is this the case? Are the sample and theoretical (Binomial) probabilities less or more similar now (n=9), compared to the values we got when n=3?
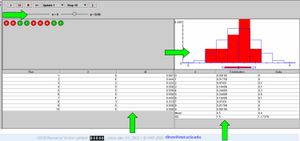
Of course, we are doing random sampling, so nothings is guaranteed, unless we ran a large number of coin tosses (say > 50) which you can do by setting n=50 and pressing the Run button. How close to the theoretical p is now the empirical sample proportion of Heads (Column M)? These should be very close.
- Common Misconceptions regarding the LLN:
- Misconception 1: If we observe a streak of 10 consecutive heads (when p=0.5, say) the odds of the 11th trial being a Head is > p! This is of course, incorrect, as the coin tosses are independent trials (an example of a memoryless process).
- Misconception 2: If run large number of coin tosses, the number of heads and number of tails become more and more equal. This is incorrect, as the LLN only guarantees that the sample proportion of heads will converge to the true population proportion (the p parameter that we selected). In fact, the difference |Heads - Tails| diverges!
Exercise 3
Much like we did above with coin tosses, one can see the action of the LLN in a variety of situations where one samples and looks for consistency of probabilities of various events (theoretically vs. empirically). Such examples may include Cards and Coins Experiments, Dice Experiments, etc.
Let's try the Ball and Urn Experiment. Go to the SOCR Experiments and select the this experiment in the drop-down list. Select N (population size), R (number of Red balls <=N) and n (sample-size, number of balls to draw from the urn. Note that you can sample with (Binomial) or without (Hypergeometric) replacement). Notice the blue model distribution of Y, the Number of Red balls in the sample of n balls, in the right panel. Again, in Red we see the sampling distribution of Y, as we do this experiment repeatedly. The probability of drawing a Red ball will depend on whether we replace the balls and the proportion of Red balls in the urn. For example, if R increases, the distribution moves to the right and become concentrated at the right end (i.e., left-skewed). Analogously, if you decrease R, the distribution will become skewed to the right and centered in the left end of the range of Y (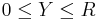 ).
).
Try repeating what we did in the Coin Toss Exercise above and see the effects of the LLN in this situation (with respect to the sample size n).
Part I of this activity contains the introductory materials
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
