SOCR BivariateNormal JS Activity
From Socr
(Difference between revisions)
(→Experiment 2: Inflation vs. HPI) |
(→Experiment 2: Inflation vs. HPI) |
||
| Line 54: | Line 54: | ||
Use the [[SOCR_Data_MonetaryBaseStocksInterest1959_2009|SOCR Inflation vs. Housing Price Index (HPI) dataset]]. | Use the [[SOCR_Data_MonetaryBaseStocksInterest1959_2009|SOCR Inflation vs. Housing Price Index (HPI) dataset]]. | ||
* Motivation: There are intricate associations between different social and economic factors like inflation, interest rate, consumer price index and housing price index. We can explore how marginal parameters for each of the ''Inflation'' and ''HPI'' distributions, and their correlation, affect their joint and conditional probabilities? | * Motivation: There are intricate associations between different social and economic factors like inflation, interest rate, consumer price index and housing price index. We can explore how marginal parameters for each of the ''Inflation'' and ''HPI'' distributions, and their correlation, affect their joint and conditional probabilities? | ||
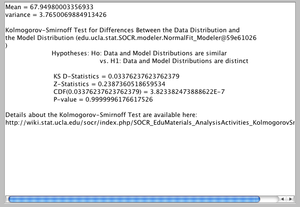
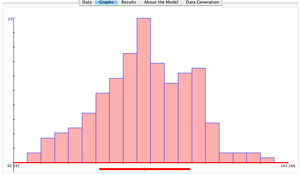
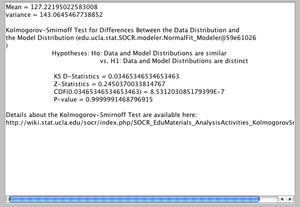
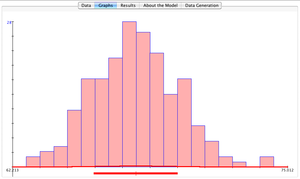
| - | * ''Caution'': This example is a little different from the [[SOCR_BivariateNormal_JS_Activity#Experiment_1:_Height_vs._Weight|human height and weight experiment above]]. In general, HPI and inflation may not follow normal distributions and may be skewed. Use the [http://socr.ucla.edu/htmls/SOCR_Charts.html SOCR Histogram Chart] to plot their distributions. Can the [http://socr.ucla.edu/htmls/HTML5/BivariateNormal/ Bivariate Normal Distribution] be used as an approximate model of the bivariate relation/probabilities of inflation and HPI? How about if we apply a [[SOCR_EduMaterials_Activities_PowerTransformFamily_Graphs|data transformation]]? For example, the figure below shows the result of applying a | + | * ''Caution'': This example is a little different from the [[SOCR_BivariateNormal_JS_Activity#Experiment_1:_Height_vs._Weight|human height and weight experiment above]]. In general, HPI and inflation may not follow normal distributions and may be skewed. Use the [http://socr.ucla.edu/htmls/SOCR_Charts.html SOCR Histogram Chart] to plot their distributions. Can the [http://socr.ucla.edu/htmls/HTML5/BivariateNormal/ Bivariate Normal Distribution] be used as an approximate model of the bivariate relation/probabilities of inflation and HPI? How about if we apply a [[SOCR_EduMaterials_Activities_PowerTransformFamily_Graphs|data transformation]]? For example, the figure below shows the result of applying a square-root-transformation to the ''inflation'' variable (\(\lambda=0.5\)). The blue distribution of the transformed data is closer to Normal (note the [[AP_Statistics_Curriculum_2007_Distrib_MeanVar#Notable_Moments|skewness and kurtosis]]) compared to the red histogram of the raw inflation values.[[Image:SOCR_BivariateNormal_JS_Activity_Fig4.png|300px]] |
* Use the [http://socr.ucla.edu/htmls/SOCR_Modeler.html SOCR Modeler] and the [[SOCR_EduMaterials_ModelerActivities_NormalBetaModelFit|SOCR Modeler activity]] to estimate the mean and standard deviation of each of the 2 variables (inflation and HPI). | * Use the [http://socr.ucla.edu/htmls/SOCR_Modeler.html SOCR Modeler] and the [[SOCR_EduMaterials_ModelerActivities_NormalBetaModelFit|SOCR Modeler activity]] to estimate the mean and standard deviation of each of the 2 variables (inflation and HPI). | ||
* Use the [http://www.socr.ucla.edu/htmls/ana/SimpleRegression_Analysis.html SOCR Simple Linear Regression applet], and the corresponding [[SOCR_EduMaterials_AnalysisActivities_SLR|activity]], to estimate the correlation (\(\rho=Corr(Inflation,HPI)\)). | * Use the [http://www.socr.ucla.edu/htmls/ana/SimpleRegression_Analysis.html SOCR Simple Linear Regression applet], and the corresponding [[SOCR_EduMaterials_AnalysisActivities_SLR|activity]], to estimate the correlation (\(\rho=Corr(Inflation,HPI)\)). | ||
Revision as of 00:57, 25 July 2012
Contents |
SOCR Educational Materials - Activities - SOCR Bivariate Normal Distribution Activity
This activity represents a 3D rendering of the Bivariate Normal Distribution. It is implemented in HTML5/JavaScript and should be portable on any computer, operating system and web-browser.
Goals
The aims of this activity are to:
- To clarify the definitions and interplay between marginal, conditional and joint probability distributions (in the bivariate Normal case)
- To learn how to calculate Normal marginal conditional and joint probabilities.
- To demonstrate that when X and Y have joint bivariate normal distribution with zero correlation, then X and Y must be independent.
Background
- In general, when X and Y are jointly continuous random variables with a joint density \(ƒ_{X,Y}(x,y)\), if A and B (non-trivial) are subsets of the ranges of X and Y (e.g., intervals), then:
- \( P(X \in A \mid Y \in B) = \frac{\int_{y\in B}\int_{x\in A} f_{X,Y}(x,y)\,dx\,dy}{\int_{y\in B}\int_{x\in\Omega} f_{X,Y}(x,y)\,dx\,dy}. \)
- In the special case where B={y0}, representing a single point, the conditional probability is:
- \( P(X \in A \mid Y = y_0) = \frac{\int_{x\in A} f_{X,Y}(x,y_0)\,dx}{\int_{x\in\Omega} f_{X,Y}(x,y_0)\,dx}\). If the set (range) A is trivial, then the conditional probability is zero.
- Suppose that X has normal distribution, the conditional mean of X given \(Y=y_o\), \(E(X|Y=y_o)\), is linear in Y, and the conditional variance of X given \(y_o\), \(Var(X|y_0)\), is constant. Then, the conditional probability distribution of X given Y = \(y_0\), \(f_{X|Y=y_o}\), is given by:
- \( f_{X|y_o} \sim N \left ( \mu_{X|y_o} = \mu_X +\rho \frac{\sigma_X}{\sigma_Y}(y_o-\mu_Y), \sigma_{X|y_o}^2 = \sigma_X^2(1-\rho^2) \right) \), where
- \( X \sim N (\mu_X, \sigma_X^2) \),
- \( E(Y)=\mu_Y\), and \(VAR(Y)=E(Y^2)-\mu_Y^2 = \sigma_Y^2 \), but this does not necessarily require that Y is normally distributed itself!
- \( \rho = Corr(X,Y)\) is the correlation between X and Y.
- This expression of the density assumes that the conditional mean of X given \(y_o\) is linear in y and the conditional variance of X given \(y_o\) is constant.
- The above does not make assumption about the distribution of Y. Now assume Y is also normally distributed with \( Y \sim N (\mu_Y, \sigma_Y^2) \). We have 3 important observations:
- 1. The density of Y is:
- \( f_Y = \frac{1}{\sigma_Y \sqrt{2\pi}} e^{-\frac{(y-\mu_y)^2}{2\sigma_Y^2}} \),
- 2. The conditional distribution of \(X\) given \(Y = y_o\) is:
- \( g_{X|Y}(x|y) = \frac{1}{\sigma_{X|Y} \sqrt{2\pi}} e^{-\frac{(x-\mu_{X|Y})^2}{2\sigma_{X|Y}^2}} \),
- \( = \frac{1}{\sigma_X\sqrt{1-\rho^2} \sqrt{2\pi}} e^{-\frac{(x-\mu_X-\rho\frac{\sigma_X}{\sigma_Y}(Y-\mu_Y))^2}{2\sigma_X^2(1-\rho^2)}} \)
- \( g_{X|Y}(x|y) = \frac{1}{\sigma_{X|Y} \sqrt{2\pi}} e^{-\frac{(x-\mu_{X|Y})^2}{2\sigma_{X|Y}^2}} \),
- 3. The joint probability density function of \(X\) and \(Y\) is:
- \( f_{X,Y}(x,y) = g_{X|Y}(x|y)f_Y(y) = \frac{1}{\sigma_X\sigma_Y 2\pi\sqrt{1-\rho^2}} e^{-q(x,y)} \), where
- \( q(x,y) = \frac{1}{2} \frac{1}{1-\rho^2} \left ( \left ( \frac{X-\mu_X}{\sigma_X} \right )^2 -2\rho\frac{X-\mu_X}{\sigma_X}\frac{Y-\mu_Y}{\sigma_Y} +\left ( \frac{Y-\mu_Y}{\sigma_Y} \right )^2 \right ) \).
- \( f_{X,Y}(x,y) = g_{X|Y}(x|y)f_Y(y) = \frac{1}{\sigma_X\sigma_Y 2\pi\sqrt{1-\rho^2}} e^{-q(x,y)} \), where
Requirements
A modern web-browser with HTML and JavaScript support is required (mobile devices should be fine). The 3D view of the bivariate Normal distribution requires WebGL support, however this is not absolutely necessary. If you toggle off the "Use WebGL" check-box in the Settings panel you can view the 3D grid/mesh representation of the 2D Normal/Gaussian distribution without WebGL.
- Go to the SOCR Bivariate Normal Distribution Webapp.
- Use the Settings to initialize the web-app.
- In the Control panel:
- Select the appropriate bivariate limits for the X and Y variables.
- Choose desired Marginal or Conditional probability function.
- 1D Normal Distribution graph will be shown to the right.
- You can rotate and manipulate the bivariate normal distribution in 3D by clicking and dragging on the graph below.
- Probability Results are reported in the bottom text area.
Experiment 1: Height vs. Weight
Use the SOCR Height vs. Weight dataset.
- Motivation: Human heights and weights are correlated, how do the marginal parameters for each of the height and weight distributions, and their correlation, affect the joint and conditional probabilities?
- Use the SOCR Modeler and the SOCR Modeler activity to estimate the mean and standard deviation of each of the 2 variables (people's heights and weights).
- Use the SOCR Simple Linear Regression applet, and the corresponding activity, to estimate the correlation (\(\rho=Corr(Height, Weight)\)).
- Use these 5 estimated quantities to apply the SOCR BVN Webapp to compute various probabilities of interest (phrased in the context of the data itself!):
- Marginal (e.g., \(P(Weight<150)\)),
- Conditional (e.g., \(P(Weight<150 \vert Height<63)\)),
- Joint (e.g., \(P(Height>60 \cap Weight<160)\)).
Experiment 2: Inflation vs. HPI
Use the SOCR Inflation vs. Housing Price Index (HPI) dataset.
- Motivation: There are intricate associations between different social and economic factors like inflation, interest rate, consumer price index and housing price index. We can explore how marginal parameters for each of the Inflation and HPI distributions, and their correlation, affect their joint and conditional probabilities?
- Caution: This example is a little different from the human height and weight experiment above. In general, HPI and inflation may not follow normal distributions and may be skewed. Use the SOCR Histogram Chart to plot their distributions. Can the Bivariate Normal Distribution be used as an approximate model of the bivariate relation/probabilities of inflation and HPI? How about if we apply a data transformation? For example, the figure below shows the result of applying a square-root-transformation to the inflation variable (\(\lambda=0.5\)). The blue distribution of the transformed data is closer to Normal (note the skewness and kurtosis) compared to the red histogram of the raw inflation values.
- Use the SOCR Modeler and the SOCR Modeler activity to estimate the mean and standard deviation of each of the 2 variables (inflation and HPI).
- Use the SOCR Simple Linear Regression applet, and the corresponding activity, to estimate the correlation (\(\rho=Corr(Inflation,HPI)\)).
- Use these 5 estimated quantities to apply the SOCR BVN Webapp to compute various probabilities of interest (phrased in the context of the data itself!):
- Marginal (e.g., \(P(Inflation<2.0)\)),
- Conditional (e.g., \(P(Inflation>5.0 \vert HPI <108)\)),
- Joint (e.g., \(P(Inflation>4.0 \cap HPI<110)\)).
References
- See the EBook Multivariate Normal Distribution Chapter
- Dinov, ID, Christou, N and Sanchez, J. (2008) Central Limit Theorem: New SOCR Applet and Demonstration Activity, Journal of Statistics Education, Volume 16, Number 2.
Translate this page: