Probability and statistics EBook
From Socr
This is a General Statistics Curriculum E-Book, which includes Advanced-Placement (AP) materials.
Preface
This is an Internet-based probability and statistics E-Book. The materials, tools and demonstrations presented in this E-Book would be very useful for advanced-placement (AP) statistics educational curriculum. The E-Book is initially developed by the UCLA Statistics Online Computational Resource (SOCR). However, all statistics instructors, researchers and educators are encouraged to contribute to this project and improve the content of these learning materials.
There are 4 novel features of this specific Statistics EBook. It is community-built, completely open-access (in terms of use and contributions), blend of technology concepts and multi-lingual.
Format
Follow the instructions in this page to expand, revise or improve the materials in this E-Book.
Learning and Instructional Usage
This section describes the means of traversing, searching, discovering and utilizing the SOCR Statistics EBook resources in formal curricula or informal learning setting. There are problems included for each section.
Chapter I: Introduction to Statistics
The Nature of Data and Variation
Although natural phenomena in real life are unpredictable, the designs of experiments are bound to generate data that varies because of intrinsic (internal to the system) or extrinsic (due to the ambient environment) effects. How many natural processes or phenomena in real life can we describe that have an exact mathematical closed-form description and are completely deterministic? How do we model the rest of the processes that are unpredictable and have random characteristics?
Uses and Abuses of Statistics
Statistics is the science of variation, randomness and chance. As such, statistics is different from other sciences, where the processes being studied obey exact deterministic mathematical laws. Statistics provides quantitative inference represented as long-time probability values, confidence or prediction intervals, odds, chances, etc., which may ultimately be subjected to varying interpretations. The phrase Uses and Abuses of Statistics refers to the notion that in some cases statistical results may be used as evidence to seemingly opposite theses. However, most of the time, common principles of logic allow us to disambiguate the obtained statistical inference.
Design of Experiments
Design of experiments is the blueprint for planning a study or experiment, performing the data collection protocol and controlling the study parameters for accuracy and consistency. Data, or information, is typically collected in regard to a specific process or phenomenon being studied to investigate the effects of some controlled variables (independent variables or predictors) on other observed measurements (responses or dependent variables). Both types of variables are associated with specific observational units (living beings, components, objects, materials, etc.)
Statistics with Tools (Calculators and Computers)
All methods for data analysis, understanding or visualizing are based on models that often have compact analytical representations (e.g., formulas, symbolic equations, etc.) Models are used to study processes theoretically. Empirical validations of the utility of models are achieved by inputting data and executing tests of the models. This validation step may be done manually, by computing the model prediction or model inference from recorded measurements. This process may be possible by hand, but only for small numbers of observations (<10). In practice, we write (or use existent) algorithms and computer programs that automate these calculations for better efficiency, accuracy and consistency in applying models to larger datasets.
Chapter II: Describing, Exploring, and Comparing Data
Types of Data
There are two important concepts in any data analysis - Population and Sample. Each of these may generate data of two major types - Quantitative or Qualitative measurements.
Summarizing Data with Frequency Tables
There are two important ways to describe a data set (sample from a population) - Graphs or Tables.
Pictures of Data
There are many different ways to display and graphically visualize data. These graphical techniques facilitate the understanding of the dataset and enable the selection of an appropriate statistical methodology for the analysis of the data.
Measures of Central Tendency
There are three main features of populations (or sample data) that are always critical in understanding and interpreting their distributions - Center, Spread and Shape. The main measures of centrality are Mean, Median and Mode(s).
Measures of Variation
There are many measures of (population or sample) spread, e.g., the range, the variance, the standard deviation, mean absolute deviation, etc. These are used to assess the dispersion or variation in the population.
Measures of Shape
The shape of a distribution can usually be determined by looking at a histogram of a (representative) sample from that population; Frequency Plots, Dot Plots or Stem and Leaf Displays may be helpful.
Statistics
Variables can be summarized using statistics - functions of data samples.
Graphs and Exploratory Data Analysis
Graphical visualization and interrogation of data are critical components of any reliable method for statistical modeling, analysis and interpretation of data.
Chapter III: Probability
Probability is important in many studies and discipline because measurements, observations and findings are often influenced by variation. In addition, probability theory provides the theoretical groundwork for statistical inference.
Fundamentals
Some fundamental concepts of probability theory include random events, sampling, types of probabilities, event manipulations and axioms of probability.
Rules for Computing Probabilities
There are many important rules for computing probabilities of composite events. These include conditional probability, statistical independence, multiplication and addition rules, the law of total probability and the Bayesian rule.
Probabilities Through Simulations
Many experimental setting require probability computations of complex events. Such calculations may be carried out exactly, using theoretical models, or approximately, using estimation or simulations.
Counting
There are many useful counting principles (including permutations and combinations) to compute the number of ways that certain arrangements of objects can be formed. This allows counting-based estimation of complex events' probabilities.
Chapter IV: Probability Distributions
There are two basic types of processes that we observe in nature - Discrete and Continuous. We begin by discussing several important discrete random processes, emphasizing the different distributions, expectations, variances and applications. In the next chapter, we will discuss their continuous counterparts. The complete list of all SOCR Distributions is available here.
Random Variables
To simplify the calculations of probabilities, we will define the concept of a random variable which will allow us to study uniformly various processes with the same mathematical and computational techniques.
Expectation (Mean) and Variance
The expectation and the variance for any discrete random variable or process are important measures of Centrality and Dispersion. This section also presents the definitions of some common population- or sample-based moments.
Bernoulli and Binomial Experiments
The Bernoulli and Binomial processes provide the simplest models for discrete random experiments.
Multinomial Experiments
Multinomial processes extend the Binomial experiments for the situation of multiple possible outcomes.
Geometric, Hypergeometric, Negative Binomial and Negative Multinomial
The Geometric, Hypergeometric, Negative Binomial, and Negative Multinomial distributions provide computational models for calculating probabilities for a large number of experiment and random variables. This section presents the theoretical foundations and the applications of each of these discrete distributions.
Poisson Distribution
The Poisson distribution models many different discrete processes where the probability of the observed phenomenon is constant in time or space. Poisson distribution may be used as an approximation to the Binomial distribution.
Chapter V: Normal Probability Distribution
The Normal Distribution is perhaps the most important model for studying quantitative phenomena in the natural and behavioral sciences - this is due to the Central Limit Theorem. Many numerical measurements (e.g., weight, time, etc.) can be well approximated by the normal distribution.
The Standard Normal Distribution
The Standard Normal Distribution is the simplest version (zero-mean, unit-standard-deviation) of the (General) Normal Distribution. Yet, it is perhaps the most frequently used version because many tables and computational resources are explicitly available for calculating probabilities.
Nonstandard Normal Distribution: Finding Probabilities
In practice, the mechanisms underlying natural phenomena may be unknown, yet the use of the normal model can be theoretically justified in many situations to compute critical and probability values for various processes.
Nonstandard Normal Distribution: Finding Scores (Critical Values)
In addition to being able to compute probability (p) values, we often need to estimate the critical values of the Normal Distribution for a given p-value.
Chapter VI: Relations Between Distributions
In this chapter, we will explore the relationships between different distributions. This knowledge will help us to compute difficult probabilities using reasonable approximations and identify appropriate probability models, graphical and statistical analysis tools for data interpretation. The complete list of all SOCR Distributions is available here and the Distributome applet provides an interactive graphical interface for exploring the relations between different distributions.
The Central Limit Theorem
The exploration of the relations between different distributions begins with the study of the sampling distribution of the sample average. This will demonstrate the universally important role of normal distribution.
Law of Large Numbers
Suppose the relative frequency of occurrence of one event whose probability to be observed at each experiment is p. If we repeat the same experiment over and over, the ratio of the observed frequency of that event to the total number of repetitions converges towards p as the number of experiments increases. Why is that and why is this important?
Normal Distribution as Approximation to Binomial Distribution
Normal Distribution provides a valuable approximation to Binomial when the sample sizes are large and the probability of successes and failures is not close to zero.
Poisson Approximation to Binomial Distribution
Poisson provides an approximation to Binomial Distribution when the sample sizes are large and the probability of successes or failures is close to zero.
Binomial Approximation to Hypergeometric
Binomial Distribution is much simpler to compute, compared to Hypergeometric, and can be used as an approximation when the population sizes are large (relative to the sample size) and the probability of successes is not close to zero.
Normal Approximation to Poisson
The Poisson can be approximated fairly well by Normal Distribution when λ is large.
Chapter VII: Point and Interval Estimates
Estimation of population parameters is critical in many applications. Estimation is most frequently carried in terms of point-estimates or interval (range) estimates for population parameters that are of interest.
Method of Moments and Maximum Likelihood Estimation
There are many ways to obtain point (value) estimates of various population parameters of interest, using observed data from the specific process we study. The method of moments and the maximum likelihood estimation are among the most popular ones frequently used in practice.
Estimating a Population Mean: Large Samples
This section discusses how to find point and interval estimates when the sample-sizes are large.
Estimating a Population Mean: Small Samples
Next, we discuss point and interval estimates when the sample-sizes are small. Naturally, the point estimates are less precise and the interval estimates produce wider intervals, compared to the case of large-samples.
Student's T distribution
The Student's T-Distribution arises in the problem of estimating the mean of a normally distributed population when the sample size is small and the population variance is unknown.
Estimating a Population Proportion
Normal Distribution is an appropriate model for proportions, when the sample size is large enough. In this section, we demonstrate how to obtain point and interval estimates for population proportion.
Estimating a Population Variance
In many processes and experiments, controlling the amount of variance is of critical importance. Thus the ability to assess variation, using point and interval estimates, facilitates our ability to make inference, revise manufacturing protocols, improve clinical trials, etc.
Confidence Intervals Activity
This activity demonstrates the usage and functionality of SOCR General Confidence Interval Applet. This applet is complementary to the SOCR Simple Confidence Interval Applet and its corresponding activity.
Chapter VIII: Hypothesis Testing
Hypothesis Testing is a statistical technique for decision making regarding populations or processes based on experimental data. It quantitatively answers the possibility that chance alone might be responsible for the observed discrepancies between a theoretical model and the empirical observations.
Fundamentals of Hypothesis Testing
In this section, we define the core terminology necessary to discuss Hypothesis Testing (Null and Alternative Hypotheses, Type I and II errors, Sensitivity, Specificity, Statistical Power, etc.)
Testing a Claim about a Mean: Large Samples
As we already saw how to construct point and interval estimates for the population mean in the large sample case, we now show how to do hypothesis testing in the same situation.
Testing a Claim about a Mean: Small Samples
We continue with the discussion on inference for the population mean of small samples.
Testing a Claim about a Proportion
When the sample size is large, the sampling distribution of the sample proportion 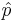 is approximately Normal, by CLT. This helps us formulate hypothesis testing protocols and compute the appropriate statistics and p-values to assess significance.
is approximately Normal, by CLT. This helps us formulate hypothesis testing protocols and compute the appropriate statistics and p-values to assess significance.
Testing a Claim about a Standard Deviation or Variance
The significance testing for the variation or the standard deviation of a process, a natural phenomenon or an experiment is of paramount importance in many fields. This chapter provides the details for formulating testable hypotheses, computation, and inference on assessing variation.
Chapter IX: Inferences From Two Samples
In this chapter, we continue our pursuit and study of significance testing in the case of having two populations. This expands the possible applications of one-sample hypothesis testing we saw in the previous chapter.
Inferences About Two Means: Dependent Samples
We need to clearly identify whether samples we compare are Dependent or Independent in all study designs. In this section, we discuss one specific dependent-samples case - Paired Samples.
Inferences About Two Means: Independent Samples
Independent Samples designs refer to experiments or observations where all measurements are individually independent from each other within their groups and the groups are independent. In this section, we discuss inference based on independent samples.
Comparing Two Variances
In this section, we compare variances (or standard deviations) of two populations using randomly sampled data.
Inferences about Two Proportions
This section presents the significance testing and inference on equality of proportions from two independent populations.
Chapter X: Correlation and Regression
Many scientific applications involve the analysis of relationships between two or more variables involved in a process of interest. We begin with the simplest of all situations where Bivariate Data (X and Y) are measured for a process and we are interested in determining the association, relation or an appropriate model for these observations (e.g., fitting a straight line to the pairs of (X,Y) data).
Correlation
The Correlation between X and Y represents the first bivariate model of association which may be used to make predictions.
Regression
We are now ready to discuss the modeling of linear relations between two variables using Regression Analysis. This section demonstrates this methodology for the SOCR California Earthquake dataset.
Variation and Prediction Intervals
In this section, we discuss point and interval estimates about the slope of linear models.
Multiple Regression
Now, we are interested in determining linear regressions and multilinear models of the relationships between one dependent variable Y and many independent variables Xi.
Chapter XI: Analysis of Variance (ANOVA)
One-Way ANOVA
We now expand our inference methods to study and compare k independent samples. In this case, we will be decomposing the entire variation in the data into independent components.
Two-Way ANOVA
Now we focus on decomposing the variance of a dataset into (independent/orthogonal) components when we have two (grouping) factors. This procedure called Two-Way Analysis of Variance.
Chapter XII: Non-Parametric Inference
To be valid, many statistical methods impose (parametric) requirements about the format, parameters and distributions of the data to be analyzed. For instance, the Independent T-Test requires the distributions of the two samples to be Normal, whereas Non-Parametric (distribution-free) statistical methods are often useful in practice, and are less-powerful.
Differences of Medians (Centers) of Two Paired Samples
The Sign Test and the Wilcoxon Signed Rank Test are the simplest non-parametric tests which are also alternatives to the One-Sample and Paired T-Test. These tests are applicable for paired designs where the data is not required to be normally distributed.
Differences of Medians (Centers) of Two Independent Samples
The Wilcoxon-Mann-Whitney (WMW) Test (also known as Mann-Whitney U Test, Mann-Whitney-Wilcoxon Test, or Wilcoxon rank-sum Test) is a non-parametric test for assessing whether two samples come from the same distribution.
Differences of Proportions of Two Samples
Depending upon whether the samples are dependent or independent, we use different statistical tests.
Differences of Means of Several Independent Samples
We now extend the multi-sample inference which we discussed in the ANOVA section, to the situation where the ANOVA assumptions are invalid.
Differences of Variances of Independent Samples (Variance Homogeneity)
There are several tests for variance equality in k samples. These tests are commonly known as tests for Homogeneity of Variances.
Chapter XIII: Multinomial Experiments and Contingency Tables
Multinomial Experiments: Goodness-of-Fit
The Chi-Square Test is used to test if a data sample comes from a population with specific characteristics.
Contingency Tables: Independence and Homogeneity
The Chi-Square Test may also be used to test for independence (or association) between two variables.
Chapter XIV:Bayesian Statistics
Preliminaries
This section will establish the groundwork for Bayesian Statistics. Probability, Random Variables, Means, Variances, and the Bayes’ Theorem will all be discussed.
Bayesian Inference for the Normal Distribution
In this section, we will provide the basic framework for Bayesian statistical inference. Generally, we take some prior beliefs about some hypothesis and then modify these prior beliefs, based on some data that we collect, in order to arrive at posterior beliefs. Another way to think about Bayesian Inference is that we are using new evidence or observations to update the probability that a hypothesis is true.
Some Other Common Distributions
This section explains the binomial, poisson, and uniform distributions in terms of Bayesian Inference.
Hypothesis Testing
This section will talk about both the classical approach to hypothesis testing and also the Bayesian approach.
Two Sample Problems
This section discusses two sample problems, with variances unknown, both equal and unequal. The Behrens-Fisher controversy is also discussed.
Hierarchical Models
Hierarchical linear models are statistical models of parameters that vary at more than a level. These models are seen as generalizations of linear models and may extend to non-linear models. Any underlying correlations in the particular model must be represented in analysis for correct inference to be drawn.
The Gibbs Sampler and Other Numerical Methods
Topics covered will include Monte Carlo Methods, Markov Chains, the EM Algorithm, and the Gibbs Sampler.
Additional EBook Chapters (under Development)
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:

